32^a Si hyperbolen duae lineae tangentes coincidant et per tactus linea producatur: perque concursum tangentium ducatur linea penes tactus coniungentem: atque per medium punctum iungentis tactus agatur linea penes unam non tangentium; recepta inter medium punctum et aequidistantem iungenti tactus per aequalia secabitur a periferia sectionis.

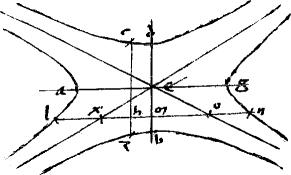
220 Sit hyperbole abg. // Centrum d. // Non tangens de. // Tangentes azg. // Iungens tactus ag. // Iungatur zd et producatur ad hbt ut ipsi ag incidat apud t. // Erit namque, per 30^am 2ⁱ Conicorum t medium punctum ipsius ag. // Item ducatur zc aequidistans ipsi ag. // Et ipsi de aequidistans tlc secans periferiam hyperboles apud l. 221 // Dico iam quod ipsa tc per aequalia secatur apud l. [A:83v] // Ducatur enim penes ag ipsae lm be. // Eritque, ut in 30 praemissa ostensum est; eadem utique ratio db be atque zm ml nec non hmb ml. // Quare et per 9^am quinti Euclidis hmb aequale ³³⁷ zm³³⁸ // Est autem, per 37^am primi Conicorum, tdz aequale db.

222 // Igitur hmb db simul aequalia sunt tdz zm .

// Sed per 6am secundi Euclidis hmb db simul aequalia sunt dm.

// Ergo tdz zm simul aequalia sunt dm.

223 // Quam ob rem, per lemma, quod praecessit 30^am huius, tz per medium secatur apud m. // Cumque lm aequidistet ipsi cz iam per 2^am sexti Euclidis. Et ipsa tc similiter per aequalia secatur apud l. // Quippe quod fuerat demonstrandum.