// Lemma
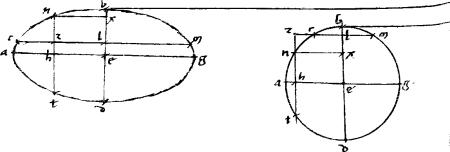
Esto linea mz secta in tria mn nd dz sitque ![]() mzd cum
mzd cum ![]() dn simul aequale316
dn simul aequale316 ![]() zn.
205
// Dico iam quod md per medium secatur apud n.
zn.
205
// Dico iam quod md per medium secatur apud n.
// Secus enim sit k punctum mediae317 sectionis.
|
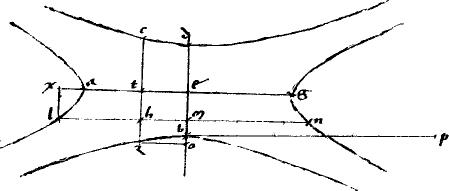
30a Si hyperbolen duae lineae tangentes coincidant, et tactus linea325 coniungat326: quae a concursu tangentium penes unam non tangentium ad tactus coniungentem, linea ducitur, per aequalia secatur a periferia sectionis.
208
Sit hyperbole abg. // Non tangentes ezh. // Tangentes adg. // Coniungens tactus ag. // Cui apud l incidat dcl aequidistans ipsi ze, quae, per 13am 2i in uno puncto coincidet sectioni, ut apud c. // Dico iam quod dl per medium secatur apud c.
209
// Coniungatur enim dz et producatur: sitque bz aequalis zt. // Et ordinate agantur be cn. // Eritque, propter similitudinem et proportionem triangulorum ![]() dn
dn ![]()
![]() nc sicut
nc sicut ![]() zb
zb ![]()
![]() be et ideo, sicut tb
be et ideo, sicut tb ![]() rectam quandoquidem327 dupla sunt dimidiis proportionalia. // Et per 21am primi Conicorum sicut
rectam quandoquidem327 dupla sunt dimidiis proportionalia. // Et per 21am primi Conicorum sicut ![]() tnb
tnb ![]()
![]() nc. //
210
Quare per 9am quinti Euclidis
nc. //
210
Quare per 9am quinti Euclidis ![]() tnb aequale est
tnb aequale est ![]() dn. // Est autem, per 37am primi Conicorum
dn. // Est autem, per 37am primi Conicorum ![]() mzd aequale
mzd aequale ![]() zb. // Quandoquidem ad tangens et am applicata328 . // Ergo
zb. // Quandoquidem ad tangens et am applicata328 . // Ergo ![]() tnb cum
tnb cum ![]() zb simul aequale est329
zb simul aequale est329 ![]() mzd et
mzd et ![]() dn simul sumptis. // Sed per 6am 2i Euclidis
dn simul sumptis. // Sed per 6am 2i Euclidis ![]() tnb cum
tnb cum ![]() zb aequale est
zb aequale est ![]() zn. // Igitur et
zn. // Igitur et ![]() zn [S:111] aequale fit ipsis
zn [S:111] aequale fit ipsis ![]() mzd
mzd ![]() 330 dn simul.
211
// Quam ob rem per lemma praemissum [A:82v] ipsa md per medium secatur apud n. // Cumque cn lm sint aequidistantes; iam per 2am 6i Euclidis et ipsa dl per aequalia similiter secatur apud c. // Id scilicet, quod proponebatur demonstrandum.
330 dn simul.
211
// Quam ob rem per lemma praemissum [A:82v] ipsa md per medium secatur apud n. // Cumque cn lm sint aequidistantes; iam per 2am 6i Euclidis et ipsa dl per aequalia similiter secatur apud c. // Id scilicet, quod proponebatur demonstrandum.