[A:81r] 28a Si in contrapositis ad coniunctionem coniugatae diametri ducantur, et dicatur301 earum quidem altera recta, altera vero transversa: ducantur autem penes ipsas duae lineae coincidentes invicem et periferiis; quadrata segmentorum ductae penes rectam, ad quadrata portionum ductae penes transversam habent eam rationem, simul scilicet accepta ad simul accepta, quam habet quadratum rectae ad quadratum transversae.
196
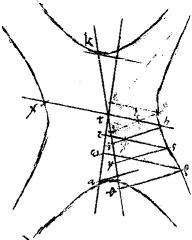
Sint ad coniunctionem contrapositae a b g d. // Centrum e. // Diametri, recta quidem aeg. // Transversa bed. // Aequidistantes ipsis ag bd ipsae lhmn zhtc. // Dico iam quod ![]()
![]() lh hn simul
lh hn simul ![]()
![]()
![]() zh hc simul sunt sicut
zh hc simul sunt sicut ![]() ag
ag ![]()
![]() bd. // Ducantur enim ordinatae lx zo ad diametros.
197
// Atque bp ad quam possunt ordinatae ad bd. Eritque per ultimam primi Conicorum, sicut pb
bd. // Ducantur enim ordinatae lx zo ad diametros.
197
// Atque bp ad quam possunt ordinatae ad bd. Eritque per ultimam primi Conicorum, sicut pb ![]() bd sic
bd sic ![]() ag
ag ![]()
![]() bd cum302 21am eiusdem erit sic etiam
bd cum302 21am eiusdem erit sic etiam ![]() zo
zo ![]()
![]() dob et sic
dob et sic ![]() gxa
gxa ![]()
![]() lx303. // Et coniunctim sicut unum ad unum, sic omnia ad omnia hoc est ut
lx303. // Et coniunctim sicut unum ad unum, sic omnia ad omnia hoc est ut ![]() ag
ag ![]()
![]() bd.
bd.
|