169
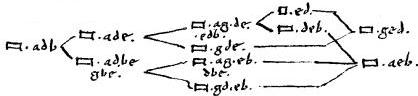
26a Si vero concursus aequidistantium apud x sit intra alteram sectionum a g ut supponitur; contentum sub portionibus aequidistantis trans[A:79r]verso, id est ![]() lxz eo rectangulo (ad quod rationem habet contentum sub portionibus aequidistantis recto, id est
lxz eo rectangulo (ad quod rationem habet contentum sub portionibus aequidistantis recto, id est ![]() rxh eam, quam, quod fit ex recta ad id, quod quod257 ex transversa) minus erit, quadrato, quod bis fit ex dimidia transversi.
rxh eam, quam, quod fit ex recta ad id, quod quod257 ex transversa) minus erit, quadrato, quod bis fit ex dimidia transversi.
170
Hoc est rectangulum quoddam258, ad quod se habet ![]() rxh sicut
rxh sicut ![]() de
de ![]()
![]() ae aequale est
ae aequale est ![]() lxz una cum
lxz una cum ![]()
![]() 259 ae. // Nam per eadem, quae in 24a premissarum, sicut
259 ae. // Nam per eadem, quae in 24a premissarum, sicut ![]() de
de ![]()
![]() ea sic
ea sic ![]() fxs
fxs ![]()
![]() cxt. // Cumque lineae hr quadrifariam divisae extrema segmenta hs fr sint, per 16am secundi, aequalia, iam per primum lemmatum 24ae praecedentis,
cxt. // Cumque lineae hr quadrifariam divisae extrema segmenta hs fr sint, per 16am secundi, aequalia, iam per primum lemmatum 24ae praecedentis, ![]() rsh sive fhs hoc est
rsh sive fhs hoc est ![]() de per 11am 2i una cum
de per 11am 2i una cum ![]() fxs aequale est
fxs aequale est ![]() rxh.
171
// Igitur et
rxh.
171
// Igitur et ![]() rxh quod est aggregatum
rxh quod est aggregatum ![]() to260 de et
to260 de et ![]() fxs
fxs ![]() aggregatum
aggregatum ![]() cxt et
cxt et ![]() ae sicut261
ae sicut261 ![]() de
de ![]()
![]() ea. // Demonstrandum igitur quod
ea. // Demonstrandum igitur quod ![]() cxt cum
cxt cum ![]() ea aequale est
ea aequale est ![]() lxz una cum
lxz una cum ![]()
![]() 262 ae. // Commune auferatur
262 ae. // Commune auferatur ![]() ae. // Et demonstrandum erit, quod
ae. // Et demonstrandum erit, quod ![]() cxt aequale est
cxt aequale est ![]() lo lxz et
lo lxz et ![]() ae.
172
// Est autem, nam cum ipsius lx quadrifariam sectae segmenta lc tz aequalia sint, per 16am secundi, iam per scholium 22ae huius
ae.
172
// Est autem, nam cum ipsius lx quadrifariam sectae segmenta lc tz aequalia sint, per 16am secundi, iam per scholium 22ae huius ![]() cxt aequale est duobus, videlicet
cxt aequale est duobus, videlicet ![]() lxz et
lxz et ![]() czt quod est
czt quod est ![]() ae, per 11am 2i. // Verum ergo, quod proponitur demonstrandum.
ae, per 11am 2i. // Verum ergo, quod proponitur demonstrandum.
Additio
173
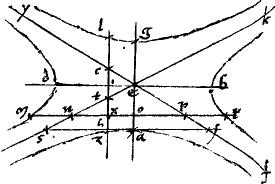
In descriptione 15ae huius, sit relictum punctum s infra diametrum xth ductisque diametris, tangentibus, aequidistantibus, caeterisque, ut ibi, suppositis et demonstratis; iam ![]() sly hic descriptum aequilaterum et aequale erit
sly hic descriptum aequilaterum et aequale erit ![]() lo sly ibi facto: itemque
lo sly ibi facto: itemque ![]() tlz huius lineationis aequilaterum et aequale erit
tlz huius lineationis aequilaterum et aequale erit ![]() lo ltz ibi lineato: propter aequidistantiam laterum parallelogrammorum nam
lo ltz ibi lineato: propter aequidistantiam laterum parallelogrammorum nam ![]() hti idem remanet.
174
// Itaque sicut ibi, ita et hic
hti idem remanet.
174
// Itaque sicut ibi, ita et hic ![]() lsy aequale etiam
lsy aequale etiam ![]() hti et
hti et ![]() tlz simul sumptis: quo fit, ut ablato utrinque in
tlz simul sumptis: quo fit, ut ablato utrinque in ![]() lqi in [A:79v] praesenti casu remaneat
lqi in [A:79v] praesenti casu remaneat ![]() rum263 htzq aequale
rum263 htzq aequale ![]() ro264 qiys quae quidem quadrilatera hic ambo sunt infra diametrum xth sicut ibi, ut in corollario265 concluditur, alterum supra, alterum infra fuerat.
175
// Sic variatur non nihil descriptio pro vario relicti puncti situ.
ro264 qiys quae quidem quadrilatera hic ambo sunt infra diametrum xth sicut ibi, ut in corollario265 concluditur, alterum supra, alterum infra fuerat.
175
// Sic variatur non nihil descriptio pro vario relicti puncti situ.
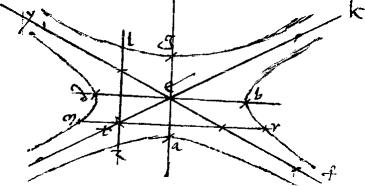
In descriptione additae praecedentis 23am huius, quadrilatera proposita sint ![]() z
z![]()
![]() s
s ![]() 266 s y
266 s y![]()
![]() singula quidem tribus rectis lineis et periferiae
singula quidem tribus rectis lineis et periferiae ![]() h s arcu conclusa (quo scilicet facilior sit et minus perplexa demonstratio) ita ut
h s arcu conclusa (quo scilicet facilior sit et minus perplexa demonstratio) ita ut ![]() [S:107] z
[S:107] z![]() et
et ![]()
![]() s infra diametrum xth ac267 infra268 centrum t diametris sint applicata.
176
// Dico quod et talia269
s infra diametrum xth ac267 infra268 centrum t diametris sint applicata.
176
// Dico quod et talia269 ![]()
![]() z
z![]()
![]() s aequalia sunt. // Agatur enim ipsi sy parallelus hi. // Eritque, per praemissam additam270 ,
s aequalia sunt. // Agatur enim ipsi sy parallelus hi. // Eritque, per praemissam additam270 , ![]() h
h![]() aequale
aequale ![]() h
h![]() . // Totum scilicet toti et271
. // Totum scilicet toti et271 ![]() st aequale
st aequale ![]() si ablatum ablato. // Igitur reliquum272
si ablatum ablato. // Igitur reliquum272 ![]()
![]() s Igitur reliquo273
s Igitur reliquo273 ![]() s
s![]() hoc est z r274 aequale est.
hoc est z r274 aequale est.
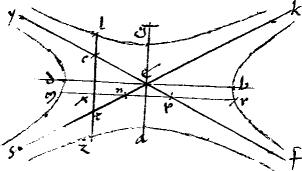
177
Item sint ![]() t
t![]()
![]() h
h ![]() 275 t i h
275 t i h![]() sub arcu periferiae communi
sub arcu periferiae communi ![]() s h et tribus rectis singula contenta, angulosque ad t centrum habentia, sub conditionibus in addita praecedente 23am huius positis. // Dico quod et talia
s h et tribus rectis singula contenta, angulosque ad t centrum habentia, sub conditionibus in addita praecedente 23am huius positis. // Dico quod et talia ![]()
![]() ra276 aequalia sunt. // Assumatur enim inter
ra276 aequalia sunt. // Assumatur enim inter ![]() h punctum quoddam utcumque relictum s et agantur lateribus quadrilaterorum paralleli sz sy.
178
// Eritque, per corollarium 15ae huius,
h punctum quoddam utcumque relictum s et agantur lateribus quadrilaterorum paralleli sz sy.
178
// Eritque, per corollarium 15ae huius, ![]() zh aequale
zh aequale ![]() si itemque
si itemque ![]() z
z![]() aequale
aequale ![]()
![]() y. // Igitur totum
y. // Igitur totum ![]() t
t![]()
![]() h aequale erit toti
h aequale erit toti ![]() t i h
t i h![]() . // Quod est propositum. // Et notandum, quod ablato communi trilatero t
. // Quod est propositum. // Et notandum, quod ablato communi trilatero t![]() h supersunt
h supersunt ![]()
![]() t
t![]()
![]() thi aequalia.
thi aequalia.
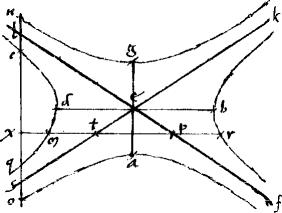
179
Adhuc sint ![]()
![]() z s
z s![]()
![]() 277 y s
277 y s![]()
![]() sub arcu periferiae communi shr278 et tribus rectis singula contenta, ita ut z s
sub arcu periferiae communi shr278 et tribus rectis singula contenta, ita ut z s ![]()
![]() latera media contineant xth diametrum, stantibus caeteris, ut in addita, quae praecedit 23am huius. // Dico quod et talia quadrilatera aequalia sunt.
180
// Agatur enim parallelus ipsis ys
latera media contineant xth diametrum, stantibus caeteris, ut in addita, quae praecedit 23am huius. // Dico quod et talia quadrilatera aequalia sunt.
180
// Agatur enim parallelus ipsis ys ![]()
![]() 279 ipsa linea hi. // Eritque per primam huius additionis
279 ipsa linea hi. // Eritque per primam huius additionis ![]() t
t![]() aequale
aequale ![]() h
h![]() 280. // Et per corollarium 15ae huius,
280. // Et per corollarium 15ae huius, ![]() zh aequale
zh aequale ![]() si281. // Igitur totum
si281. // Igitur totum ![]() z
z![]() toti
toti ![]() s
s![]() aequale est: ut proponitur.
aequale est: ut proponitur.
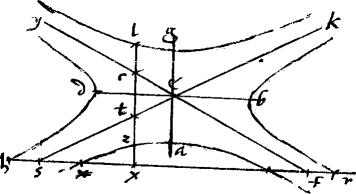
181
Sint demum ![]() z
z![]()
![]() s
s ![]() 282
282 ![]() y s
y s![]() sub arcu periferiae communi
sub arcu periferiae communi ![]() h s283 et tribus rectis singula conclusa: ita ut eorum latera
h s283 et tribus rectis singula conclusa: ita ut eorum latera ![]() z y
z y![]() quae sunt partes diametrorum, quibus applicantur, se invicem secent apud t centrum: caeteris suppositis, ut in addita praecedente 23am huius.
182
// Dico tandem quod huiusmodi quadrilatera aequalia sunt agantur enim ipsis
quae sunt partes diametrorum, quibus applicantur, se invicem secent apud t centrum: caeteris suppositis, ut in addita praecedente 23am huius.
182
// Dico tandem quod huiusmodi quadrilatera aequalia sunt agantur enim ipsis ![]()
![]() z s paralleli t
z s paralleli t![]() t h lineae et ipsis
t h lineae et ipsis ![]()
![]() y s paralleli
y s paralleli ![]()
![]() h i. Et procedatur sic. // Nam, per primam harum additarum
h i. Et procedatur sic. // Nam, per primam harum additarum ![]() ts aequale
ts aequale ![]() hy et per 3am quae est ante praemissa,
hy et per 3am quae est ante praemissa, ![]()
![]() h aequale est
h aequale est ![]()
![]() i.
183
// Igitur totum
i.
183
// Igitur totum ![]() z
z![]()
![]() s aequale iam toti
s aequale iam toti ![]() y t
y t![]() s quorum videlicet illud habet t centrum in latere z
s quorum videlicet illud habet t centrum in latere z![]() hoc vero habet idem t centrum apud angulum. // Item, per primam harum additarum,
hoc vero habet idem t centrum apud angulum. // Item, per primam harum additarum, ![]()
![]()
![]() aequale est
aequale est ![]()
![]()
![]() . // Ergo et totum
. // Ergo et totum ![]() z
z![]()
![]() s aequale sit toti
s aequale sit toti ![]()
![]() y s
y s![]() . //
184
Quandoquidem illud constat ex tribus
. //
184
Quandoquidem illud constat ex tribus ![]() 284 et hoc ex aliis tribus aequalibus: bina comparando. // Quod est propositum. Unde manifestum est, quod quadrilatera duo, de quibus primum [A:80r] agitur in corollario 15ae huius, aut habent latera, quae sunt partes diametrorum, quibus adhaerent, separatim a centro sectionum et tunc, aut unum ad unam partem a centro et alterum ad alteram: et de his agitur in addita praecedente 23am huius: aut dicta quarilatera habent ambo talia [S:108] latera ad eandem partem centri: et de his285 agitur in 2a immediate praecedentium additarum.
185
Aut habent talia latera, ut unum eorum tantum adhaereat centro, et tunc aut ita, ut centrum sit in extremo lateris propinquioris286 alteri quadrilatero et de his287 agitur in corollario 15ae huius: aut in extremo remotiore, et de his288 agitur in prima praemissarum additarum: aut ita, ut centrum sit in aliquo puncto medio lateris: et de his289 agitur in 4a praemissarum.
186
Aut habent talia latera, ut ambo adhaereant centro: et tunc, aut centrum est in extremo communi ambobus lateribus: et de his agitur in 3a praecedentium aut centrum est in coincidentia laterum et de his290 agitur in 5a earumdem immediate praecedenti.
187
Aut centrum est in extremo unius ex lateribus, et in aliquo puncto medio alterius: et de his agitur in processu demonstrationis eiusdem immediate praemissae. // Sic videmur discussisse omnem varietatem, quae circa huiusmodi quadrilatera potuisset contingere, utcumque et ubicumque aut secent se invicem, aut diametris incurrant latera.
188
// Sed quae non descriptio in conicis variando propagari posset. Hucusque Castelboni 5o maius 1547291.
284 et hoc ex aliis tribus aequalibus: bina comparando. // Quod est propositum. Unde manifestum est, quod quadrilatera duo, de quibus primum [A:80r] agitur in corollario 15ae huius, aut habent latera, quae sunt partes diametrorum, quibus adhaerent, separatim a centro sectionum et tunc, aut unum ad unam partem a centro et alterum ad alteram: et de his agitur in addita praecedente 23am huius: aut dicta quarilatera habent ambo talia [S:108] latera ad eandem partem centri: et de his285 agitur in 2a immediate praecedentium additarum.
185
Aut habent talia latera, ut unum eorum tantum adhaereat centro, et tunc aut ita, ut centrum sit in extremo lateris propinquioris286 alteri quadrilatero et de his287 agitur in corollario 15ae huius: aut in extremo remotiore, et de his288 agitur in prima praemissarum additarum: aut ita, ut centrum sit in aliquo puncto medio lateris: et de his289 agitur in 4a praemissarum.
186
Aut habent talia latera, ut ambo adhaereant centro: et tunc, aut centrum est in extremo communi ambobus lateribus: et de his agitur in 3a praecedentium aut centrum est in coincidentia laterum et de his290 agitur in 5a earumdem immediate praecedenti.
187
Aut centrum est in extremo unius ex lateribus, et in aliquo puncto medio alterius: et de his agitur in processu demonstrationis eiusdem immediate praemissae. // Sic videmur discussisse omnem varietatem, quae circa huiusmodi quadrilatera potuisset contingere, utcumque et ubicumque aut secent se invicem, aut diametris incurrant latera.
188
// Sed quae non descriptio in conicis variando propagari posset. Hucusque Castelboni 5o maius 1547291.