|
Lemma I
142
Sit linea ab in quatuor portiones sic divisa, ut, extremae ag, bd sint aequales: mediae ge, ed quantecumque. Dico iam quod  ged ged  agb pariter sumpta aequalia sunt agb pariter sumpta aequalia sunt  aeb. // Nam per primam secundi Euclidis aeb. // Nam per primam secundi Euclidis  ag, eb hoc est ag, eb hoc est  ebd cum ebd cum  geb simul aequale est199 geb simul aequale est199  aeb.
143
// Item, per eandem, aeb.
143
// Item, per eandem,  ag ed quod est ag ed quod est  edb cum edb cum  ag db quod est quadratum utriusvis aequale est200 ag db quod est quadratum utriusvis aequale est200  ag eb sive ebd. // Nec non ag eb sive ebd. // Nec non  ge db sive age cum ge db sive age cum  ged simul aequale est ged simul aequale est  lo geb. // Igitur quatuor rectangula videtur201 lo geb. // Igitur quatuor rectangula videtur201  202 ag db 202 ag db  ag ed ag ed  age age  ged simul sumpta aequalia sunt ged simul sumpta aequalia sunt  aeb.
144
// Verum per eandem primam 2i aeb.
144
// Verum per eandem primam 2i  agb aequale est tribus agb aequale est tribus  lis videlicet lis videlicet  203 ag db 203 ag db  ag ed ag ed  age. // Ergo pro tribus uno posito fiet age. // Ergo pro tribus uno posito fiet  agb cum agb cum  ged aequale ged aequale  aeb. // Quod erat ostendendum. aeb. // Quod erat ostendendum.
|
|
 agb vel gbd agb vel gbd |
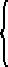 |
 ag db ag db |
|
 |
 ag eb ag eb |
vel ebd |
 |
 aeb aeb |
 ag ed ag ed |
vel edb |
 age age |
vel ge db |
 |
 geb geb |
|
 ged ged |
|
|
|
204
Lemma II
145
Item sit linea ab in ternas portiones sic divisa, ut earum extremae ag, db sint aequales: media gd quantacumque: et extremarum altera bd utcumque divisa apud e. //Hoc est, ut prima quatuor portionum ag sit aequalis postremis de, eb. //Dico iam quod  aeb aequale est sumptum cum aeb aequale est sumptum cum  ged ipsi ged ipsi  adb.
146
// Nam per primam 2i Euclidis adb.
146
// Nam per primam 2i Euclidis  adb aequale est adb aequale est  ade et ade et  ad be quod est ad be quod est  gbe simul sumptis. //Item gbe simul sumptis. //Item  ade aequale est ade aequale est  ag de quod est ag de quod est  edb et edb et  gde pariter iunctis. //Nec non gde pariter iunctis. //Nec non  ad eb sive gbe aequale est ad eb sive gbe aequale est  ag eb quod est dbe et ag eb quod est dbe et  gd eb coniunctis. //Igitur gd eb coniunctis. //Igitur  adb205 aequale est quatuor rectangulis, videlicet adb205 aequale est quatuor rectangulis, videlicet  ag de quod est edb ag de quod est edb  gde gde  ag eb quod est dbe et ag eb quod est dbe et  gd eb similiter aggregatis.
147
// Verum primum ex his206 scilicet gd eb similiter aggregatis.
147
// Verum primum ex his206 scilicet  ag de quod207 est ag de quod207 est  edb per 3am 2i Euclidis aequale est edb per 3am 2i Euclidis aequale est  de et de et  deb. //Ergo deb. //Ergo  adb aequale erit quinque rectangulis per208 primam 2i scilicet adb aequale erit quinque rectangulis per208 primam 2i scilicet  de209 de209  deb deb  gde gde  ga eb ga eb  gd eb. // Sed duo ex his, scilicet gd eb. // Sed duo ex his, scilicet  de et de et  gde simul aequalia sunt gde simul aequalia sunt  ged.
148
Tria vero reliqua ged.
148
Tria vero reliqua  deb deb  ag eb ag eb  gd eb simul sunt aequalia gd eb simul sunt aequalia  aeb. //Igitur aeb. //Igitur  aeb cum aeb cum  ged aequatur ged aequatur  adb. //Quod proponitur ostendendum. adb. //Quod proponitur ostendendum.
|
|
|
|
 |
 gde gde |
|
 |
 ged ged |
 adb adb |
 |
 ade ade |
|
 ag de ag de |
<vel> edb |
 |
 ed ed |
|
|
 deb deb |
 |
 aeb aeb |
 ad be ad be |
<vel> gbe |
 |
 ag eb ag eb |
<vel> dbe |
|
 gd eb gd eb |
|
|
|
210
149
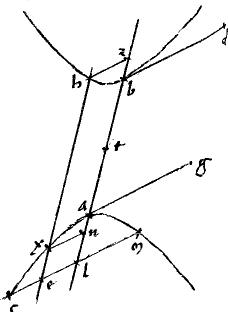
[A:77v] 24a Si in contrapositis ad coniunctionem a centro ducantur ad sectiones duae lineae, et dicatur211 ipsarum altera transversa diameter, altera recta: et agantur quaedam penes diametros coincidentes invicem et sectionibus: sitque actarum coincidentia in loco, qui est inter quatuor sectiones; contentum sub sectionibus aequidistantis lateri transverso cum eo (ad quod rationem habet, quod est sub segmentis aequidistantis recto, eam quam, [S:104] quod fit ex recta ad quadratum, quod fit ex transversa) aequale erit tetragono, quod bis sit ex dimidio transversi.
150
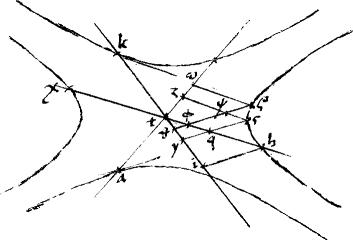
Sint contrapositae ad coniunctionem a, b, g, d. // Quarum quidem centrum e. // Transversa diameter aeg. // Recta autem212 deb. // Ipsi aeg aequidistans zhxticl213. //Ipsique deb aequidistans mnxotpr214 coincidentes apud x. //Sitque in prima descriptione punctum x intra angulum sef.
151
//Dico iam quod  zxl cum rectangulo, (ad quod rationem habet zxl cum rectangulo, (ad quod rationem habet  lum mxr quam lum mxr quam  db db   ag) aequale est ag) aequale est   215 ae. //Cum enim 215 ae. //Cum enim  sa aequale sit sa aequale sit  de per 21am 2i eadem erit ratio de per 21am 2i eadem erit ratio  216 saf 216 saf   ea et ea et  de de   ea.
152
//Ratio autem ea.
152
//Ratio autem  217 saf 217 saf   ea et ideo ratio ea et ideo ratio  de de   ea componitur quidem ea componitur quidem |
|
|
ex rationibus |
|
|
 |
sa  ae vel nx ae vel nx  xt xt |
 |
fa  ae vel px ae vel px  xc xc |
|
|
|
|
|
ex quibus componitur ratio   pxn pxn   ***218 propter similitudinem triangulorum. Igitur sicut ***218 propter similitudinem triangulorum. Igitur sicut  de de   ea sic ea sic  pxn pxn   cxt
153
Sed per 11am secundi Conicorum cxt
153
Sed per 11am secundi Conicorum  de aequale est de aequale est  pmn hoc est pmn hoc est  rnm. Itemque rnm. Itemque  ea aequale est ea aequale est  czt hoc est czt hoc est  ltz. Namque per 8am et 16am 2i ipsae mn pr sunt aequales: ipsaeque lc tz aequales. ltz. Namque per 8am et 16am 2i ipsae mn pr sunt aequales: ipsaeque lc tz aequales. |
|
154
Ergo, sicut  de de   ea sic ea sic |
|
|
 pxn pxn |
 |
 |
 |
 cxt cxt |
 rnm rnm |
 ltz hoc est ltz hoc est  czt czt |
|
|
|
|
|
|
|
|
aequale autem est per primum lemmatum praecedentium |
|
|
|
simul  rxm rxm |
|
. |
|
|
155
//Itaque sicut  de de   ea hoc est sicut ea hoc est sicut  db db   ag ag |
|
sic est  rxm rxm |
220 |
simul. |
|
|
|
|
|
Demonstrandum est igitur quod [A:78r] |
|
aequalia sunt   221 ea. 221 ea. |
|
|
//Et ablatis utrinque iam  czt czt   222 ea invicem aequalibus. 222 ea invicem aequalibus. |
|
|
Restat demonstrandum quod |
|
aequalia sunt  to ea. to ea. |
|
|
156
// Sunt autem: quoniam scilicet per secundum lemmatum praemissorum, |
|
|
ipsa |
|
aequalia sunt  lo ltz hoc est lo ltz hoc est  czt quod est223 czt quod est223  ae. ae. |
|
|
//Verum ergo est, quod proponitur demonstrandum.
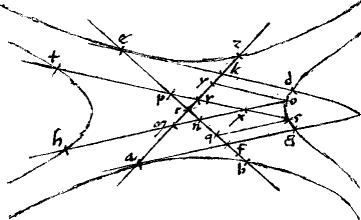
// Coincidant utique in secunda descriptione, zl mr uni nontangentium apud t.
157
// Eritque per 11am secundi Conicorum  ztl aequale ztl aequale  to ae. Itemque to ae. Itemque  mtr aequum mtr aequum  de. //Et ideo, sicut de. //Et ideo, sicut  de de   ae hoc est, sicut ae hoc est, sicut  db db   ag sic ag sic  mtr mtr   ztl. //Quare ztl. //Quare  ztl cum ipsomet ztl cum ipsomet  ztl aequum224 ztl aequum224   ae. // Id scilicet quod proponitur si attendis, in principio demonstrandum. // ae. // Id scilicet quod proponitur si attendis, in principio demonstrandum. //

158
Sit demum in tertia descriptione, punctum x intra angulum sey vel fek. //Eritque, ut in primo casu, ex memorata rationum compositione. Sicut  de de   ea sic ea sic  pxn pxn   cxt. //Sed, per 11am 2i cxt. //Sed, per 11am 2i  de aequale est de aequale est  pmn hoc est pmn hoc est  rnm. //Itemque rnm. //Itemque  ae aequale ae aequale  ltz.
159
//Igitur sicut ltz.
159
//Igitur sicut  rnm rnm   ltz totum scilicet ad totum, sic ltz totum scilicet ad totum, sic  pxn pxn   cxt (cum videlicet, per secundum lemmatum, cxt (cum videlicet, per secundum lemmatum,  rxm cum rxm cum  pxn aequum sit225 pxn aequum sit225  rnm) ablatum ad ablatum.
160
//Quare et reliquum ad reliquum, hoc est ipsum, rnm) ablatum ad ablatum.
160
//Quare et reliquum ad reliquum, hoc est ipsum,  rxm rxm  excessum quo excessum quo  ltz (quod est ltz (quod est  ae) maius est ae) maius est  lo cxt erit sicut totum ad totum, hoc est, sicut lo cxt erit sicut totum ad totum, hoc est, sicut  rnm rnm   ltz et ideo sicut ltz et ideo sicut  de de   ea id est, sicut ea id est, sicut  db db   ag. [S:105] //Demonstrandum igitur, quod ag. [S:105] //Demonstrandum igitur, quod  zxl cum praedicto excessu, aequale est zxl cum praedicto excessu, aequale est   226 ae.
161
//Cum autem, per primum lemmatum, 226 ae.
161
//Cum autem, per primum lemmatum,  ltz cum ltz cum  cxt aequale sit cxt aequale sit  lxz. //Auferantur hinc lxz. //Auferantur hinc  ae inde vero ae inde vero  ltz iampridem aequalia. //Et restat ostendendum quod ipsum ltz iampridem aequalia. //Et restat ostendendum quod ipsum  cxt cum excessu memorato aequale est cxt cum excessu memorato aequale est  to ae. //Est autem, quoniam to ae. //Est autem, quoniam  cxt cum tali excessu aequale fuit cxt cum tali excessu aequale fuit  ltz et perinde ipsi ltz et perinde ipsi  ae. //Verum igitur quod proponebatur demonstrandum. ae. //Verum igitur quod proponebatur demonstrandum.
|
![]() ged
ged ![]() agb pariter sumpta aequalia sunt
agb pariter sumpta aequalia sunt ![]() aeb. // Nam per primam secundi Euclidis
aeb. // Nam per primam secundi Euclidis ![]() ag, eb hoc est
ag, eb hoc est ![]() ebd cum
ebd cum ![]() geb simul aequale est199
geb simul aequale est199 ![]() aeb.
143
// Item, per eandem,
aeb.
143
// Item, per eandem, ![]() ag ed quod est
ag ed quod est ![]() edb cum
edb cum ![]() ag db quod est quadratum utriusvis aequale est200
ag db quod est quadratum utriusvis aequale est200 ![]() ag eb sive ebd. // Nec non
ag eb sive ebd. // Nec non ![]() ge db sive age cum
ge db sive age cum ![]() ged simul aequale est
ged simul aequale est ![]() lo geb. // Igitur quatuor rectangula videtur201
lo geb. // Igitur quatuor rectangula videtur201 ![]() 202 ag db
202 ag db ![]() ag ed
ag ed ![]() age
age ![]() ged simul sumpta aequalia sunt
ged simul sumpta aequalia sunt ![]() aeb.
144
// Verum per eandem primam 2i
aeb.
144
// Verum per eandem primam 2i ![]() agb aequale est tribus
agb aequale est tribus ![]() lis videlicet
lis videlicet ![]() 203 ag db
203 ag db ![]() ag ed
ag ed ![]() age. // Ergo pro tribus uno posito fiet
age. // Ergo pro tribus uno posito fiet ![]() agb cum
agb cum ![]() ged aequale
ged aequale ![]() aeb. // Quod erat ostendendum.
aeb. // Quod erat ostendendum.

![]() aeb aequale est sumptum cum
aeb aequale est sumptum cum ![]() ged ipsi
ged ipsi ![]() adb.
146
// Nam per primam 2i Euclidis
adb.
146
// Nam per primam 2i Euclidis ![]() adb aequale est
adb aequale est ![]() ade et
ade et ![]() ad be quod est
ad be quod est ![]() gbe simul sumptis. //Item
gbe simul sumptis. //Item ![]() ade aequale est
ade aequale est ![]() ag de quod est
ag de quod est ![]() edb et
edb et ![]() gde pariter iunctis. //Nec non
gde pariter iunctis. //Nec non ![]() ad eb sive gbe aequale est
ad eb sive gbe aequale est ![]() ag eb quod est dbe et
ag eb quod est dbe et ![]() gd eb coniunctis. //Igitur
gd eb coniunctis. //Igitur ![]() adb205 aequale est quatuor rectangulis, videlicet
adb205 aequale est quatuor rectangulis, videlicet ![]() ag de quod est edb
ag de quod est edb ![]() gde
gde ![]() ag eb quod est dbe et
ag eb quod est dbe et ![]() gd eb similiter aggregatis.
147
// Verum primum ex his206 scilicet
gd eb similiter aggregatis.
147
// Verum primum ex his206 scilicet ![]() ag de quod207 est
ag de quod207 est ![]() edb per 3am 2i Euclidis aequale est
edb per 3am 2i Euclidis aequale est ![]() de et
de et ![]() deb. //Ergo
deb. //Ergo ![]() adb aequale erit quinque rectangulis per208 primam 2i scilicet
adb aequale erit quinque rectangulis per208 primam 2i scilicet ![]() de209
de209 ![]() deb
deb ![]() gde
gde ![]() ga eb
ga eb ![]() gd eb. // Sed duo ex his, scilicet
gd eb. // Sed duo ex his, scilicet ![]() de et
de et ![]() gde simul aequalia sunt
gde simul aequalia sunt ![]() ged.
148
Tria vero reliqua
ged.
148
Tria vero reliqua ![]() deb
deb ![]() ag eb
ag eb ![]() gd eb simul sunt aequalia
gd eb simul sunt aequalia ![]() aeb. //Igitur
aeb. //Igitur ![]() aeb cum
aeb cum ![]() ged aequatur
ged aequatur ![]() adb. //Quod proponitur ostendendum.
adb. //Quod proponitur ostendendum. 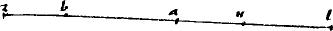

![]() zxl cum rectangulo, (ad quod rationem habet
zxl cum rectangulo, (ad quod rationem habet ![]() lum mxr quam
lum mxr quam ![]() db
db ![]()
![]() ag) aequale est
ag) aequale est ![]()
![]() 215 ae. //Cum enim
215 ae. //Cum enim ![]() sa aequale sit
sa aequale sit ![]() de per 21am 2i eadem erit ratio
de per 21am 2i eadem erit ratio ![]() 216 saf
216 saf ![]()
![]() ea et
ea et ![]() de
de ![]()
![]() ea.
152
//Ratio autem
ea.
152
//Ratio autem ![]() 217 saf
217 saf ![]()
![]() ea et ideo ratio
ea et ideo ratio ![]() de
de ![]()
![]() ea componitur quidem
ea componitur quidem 
![]() ztl aequale
ztl aequale ![]() to ae. Itemque
to ae. Itemque ![]() mtr aequum
mtr aequum ![]() de. //Et ideo, sicut
de. //Et ideo, sicut ![]() de
de ![]()
![]() ae hoc est, sicut
ae hoc est, sicut ![]() db
db ![]()
![]() ag sic
ag sic ![]() mtr
mtr ![]()
![]() ztl. //Quare
ztl. //Quare ![]() ztl cum ipsomet
ztl cum ipsomet ![]() ztl aequum224
ztl aequum224 ![]()
![]() ae. // Id scilicet quod proponitur si attendis, in principio demonstrandum. //
ae. // Id scilicet quod proponitur si attendis, in principio demonstrandum. // 
![]() de
de ![]()
![]() ea sic
ea sic ![]() pxn
pxn ![]()
![]() cxt. //Sed, per 11am 2i
cxt. //Sed, per 11am 2i ![]() de aequale est
de aequale est ![]() pmn hoc est
pmn hoc est ![]() rnm. //Itemque
rnm. //Itemque ![]() ae aequale
ae aequale ![]() ltz.
159
//Igitur sicut
ltz.
159
//Igitur sicut ![]() rnm
rnm ![]()
![]() ltz totum scilicet ad totum, sic
ltz totum scilicet ad totum, sic ![]() pxn
pxn ![]()
![]() cxt (cum videlicet, per secundum lemmatum,
cxt (cum videlicet, per secundum lemmatum, ![]() rxm cum
rxm cum ![]() pxn aequum sit225
pxn aequum sit225 ![]() rnm) ablatum ad ablatum.
160
//Quare et reliquum ad reliquum, hoc est ipsum,
rnm) ablatum ad ablatum.
160
//Quare et reliquum ad reliquum, hoc est ipsum, ![]() rxm
rxm ![]() excessum quo
excessum quo ![]() ltz (quod est
ltz (quod est ![]() ae) maius est
ae) maius est ![]() lo cxt erit sicut totum ad totum, hoc est, sicut
lo cxt erit sicut totum ad totum, hoc est, sicut ![]() rnm
rnm ![]()
![]() ltz et ideo sicut
ltz et ideo sicut ![]() de
de ![]()
![]() ea id est, sicut
ea id est, sicut ![]() db
db ![]()
![]() ag. [S:105] //Demonstrandum igitur, quod
ag. [S:105] //Demonstrandum igitur, quod ![]() zxl cum praedicto excessu, aequale est
zxl cum praedicto excessu, aequale est ![]()
![]() 226 ae.
161
//Cum autem, per primum lemmatum,
226 ae.
161
//Cum autem, per primum lemmatum, ![]() ltz cum
ltz cum ![]() cxt aequale sit
cxt aequale sit ![]() lxz. //Auferantur hinc
lxz. //Auferantur hinc ![]() ae inde vero
ae inde vero ![]() ltz iampridem aequalia. //Et restat ostendendum quod ipsum
ltz iampridem aequalia. //Et restat ostendendum quod ipsum ![]() cxt cum excessu memorato aequale est
cxt cum excessu memorato aequale est ![]() to ae. //Est autem, quoniam
to ae. //Est autem, quoniam ![]() cxt cum tali excessu aequale fuit
cxt cum tali excessu aequale fuit ![]() ltz et perinde ipsi
ltz et perinde ipsi ![]() ae. //Verum igitur quod proponebatur demonstrandum.
ae. //Verum igitur quod proponebatur demonstrandum.