[A:76v] 23a Si in contrapositis ad coniunctionem duae lineae oppositas sectiones tangentes coincidant ad unam sectionem ex duabus reliquis, ut contingit: ducantur autem ex quaedam tangentibus paralleli secantes se invicem et alteras contrapositas; erunt ad invicem tangentium quadrata sicut contenta sub portionibus parallelorum se secantium.
135
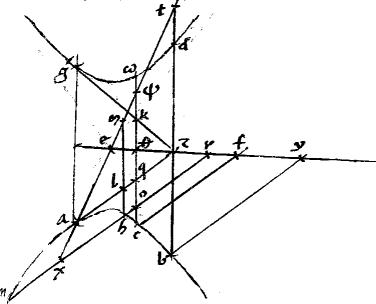
Sint ad coniunctionem contrapositae ab, gd, ze, ht. // Quarum centrum c. // Lineae quae tangunt ipsas ab ze sectiones, sint afgl, ekdl. // Et penes ipsam ag ducatur hmnxo penes autem ed ipsa tprxs se invicem secantes apud x. Et ipsi196 dg periferiae incidentes apud o, s puncta. // Dico iam quod sicut est ![]() el
el ![]()
![]() la sic
la sic ![]() txs
txs ![]()
![]() hxo.
136
// Ducantur enim per tactus diametri amcykz, epcnqfb. Itemque aequidistantes ipsi quidem ag ipsa qs ipsique ed ipsa oy. // Et quoniam tam tps ad diametrum eb quam hmo ad diametrum hmo197 ordinate applicata est. // Ideo per 16am primi Conicorum ipsae tp ps aequales sunt. Itemque ipsae hm, mo aequales. // Quare, per 5am secundi Euclidis erunt
hxo.
136
// Ducantur enim per tactus diametri amcykz, epcnqfb. Itemque aequidistantes ipsi quidem ag ipsa qs ipsique ed ipsa oy. // Et quoniam tam tps ad diametrum eb quam hmo ad diametrum hmo197 ordinate applicata est. // Ideo per 16am primi Conicorum ipsae tp ps aequales sunt. Itemque ipsae hm, mo aequales. // Quare, per 5am secundi Euclidis erunt ![]() txs cum
txs cum ![]() px similiter aequalia
px similiter aequalia ![]() ps.
137
// Sed propter similitudinem figurarum sicut
ps.
137
// Sed propter similitudinem figurarum sicut ![]() el
el ![]()
![]() efl sic
efl sic ![]() ps
ps ![]()
![]() pqs totum scilicet ad totum: et sic
pqs totum scilicet ad totum: et sic ![]() px
px ![]()
![]() pnx ablatum scilicet ad ablatum. // Igitur erit iam
pnx ablatum scilicet ad ablatum. // Igitur erit iam ![]() txs
txs ![]()
![]() qnxs reliquum quidem ad reliquum, sicut
qnxs reliquum quidem ad reliquum, sicut ![]() ps
ps ![]()
![]() pqs totum ad totum et sicut
pqs totum ad totum et sicut ![]() el
el ![]()
![]() efl. //
138
Verum ex 4a huius
efl. //
138
Verum ex 4a huius ![]() efl aequale est
efl aequale est ![]() lo akl et per praecedentem additam,
lo akl et per praecedentem additam, ![]() qnxs aequale est
qnxs aequale est ![]() xryo. // Ergo, sicut
xryo. // Ergo, sicut ![]() el
el ![]()
![]() akl sic
akl sic ![]() txs
txs ![]()
![]() xryo. // Sicut autem ostensum est quod
xryo. // Sicut autem ostensum est quod ![]() el
el ![]()
![]() efl est sicut
efl est sicut ![]() txs
txs ![]()
![]() qnxs sic ostendetur quod
qnxs sic ostendetur quod ![]() al
al ![]()
![]() akl est sicut
akl est sicut ![]() hxo
hxo ![]()
![]() xryo.
139
// Et conversim
xryo.
139
// Et conversim ![]() akl
akl ![]()
![]() al sicut
al sicut ![]() xryo
xryo ![]()
![]() hxo. // Itaque ex aequali proportione
hxo. // Itaque ex aequali proportione ![]() el
el ![]()
![]() al sicut198
al sicut198 ![]() txs
txs ![]()
![]() hxo. // Id quod iam proponebatur demonstrandum.
hxo. // Id quod iam proponebatur demonstrandum.
[S:103] Scholium
140 Notandum quod puncta contactuum a, e et puncta relicta o, s in ipsis sectionibus in quibus sunt, possunt multipliciter variari: proque talium punctorum situ tam variae descriptiones accomodari: quae tamen perspicaciae lectoris, exercitioque ingeniorum relinquuntur. 141 // Nobis satis sit citatione propositionum, correctione locorum, additione scholiorum ac corollariorum et theorematum nece[A:77r]ssariorum fecisse cuncta faciliora. // Nunc lemmata quaedam praemittemus trium sequentium propositionum demonstrationibus necessaria.