[A:72v] 18a Si contrapositas duae lineae tangentes coincidant: et relictum sit quoddam140 punctum in utravis sectionum: et ab ipso ducatur quaedam linea penes unam tangentium secans sectionem et alteram tangentem; erit, ut quae fiunt ex tangentibus quadrata ad invicem, sic contentum sub iis, quae sunt inter sectionem et tangentem, ad id, quod fit ex recepta de ipsa tangente tetragonum.
87
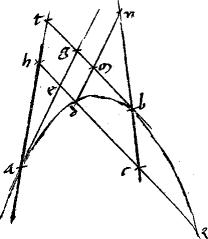
[S:97] Sint contrapositae ab, mn. // Et relictum sit in sectione mn quodvis punctum d. // Et per ipsum ducatur penes bgt tangentem 141 zodhe occurrens alteri tangenti agle apud e secans autem periferiam apud d z. // Dico iam quod erit sicut ![]() bg
bg ![]()
![]() ga sic
ga sic ![]() zed
zed ![]()
![]() ea.
88
// Ducatur enim penes ipsam ae linea dx. // Itemque per centrum k diametri atkhm et blkxno. // Eritque, per 47am primi Conicorum do aequalis oz. // Et ideo, per 6am secundi Euclidis
ea.
88
// Ducatur enim penes ipsam ae linea dx. // Itemque per centrum k diametri atkhm et blkxno. // Eritque, per 47am primi Conicorum do aequalis oz. // Et ideo, per 6am secundi Euclidis ![]() zed cum
zed cum ![]() do aequalia sunt
do aequalia sunt ![]() eo142.
89
// Et quoniam propter aequidistantiam linearum dx le et similitudinem figurarum sicut est
eo142.
89
// Et quoniam propter aequidistantiam linearum dx le et similitudinem figurarum sicut est ![]() eo
eo ![]()
![]() eol totum143 ad totum: sic
eol totum143 ad totum: sic ![]() do
do ![]()
![]() dox ablatum ad ablatum. // Ideo, per 19am quinti Euclidis sicut
dox ablatum ad ablatum. // Ideo, per 19am quinti Euclidis sicut ![]() zed
zed ![]()
![]() delx reliquum ad reliquum; sic
delx reliquum ad reliquum; sic ![]() eo
eo ![]()
![]() eol totum ad totum. // Item sicut
eol totum ad totum. // Item sicut ![]() eo
eo ![]()
![]() eol sic
eol sic ![]() bg
bg ![]()
![]() gbl propter similitudinem figurarum.
90
// Aequale autem
gbl propter similitudinem figurarum.
90
// Aequale autem ![]() 144 delx
144 delx ![]() lo aeh cum, per 9am huius,
lo aeh cum, per 9am huius, ![]() dk aequum sit
dk aequum sit ![]() lo akl145 sive per eius corollarium. // Aequale et
lo akl145 sive per eius corollarium. // Aequale et ![]() gbl
gbl ![]() lo agt per primam huius. // Igitur sicut
lo agt per primam huius. // Igitur sicut ![]() zed
zed ![]()
![]() aeh sic
aeh sic ![]() bg
bg ![]()
![]() agt. // Verum sicut
agt. // Verum sicut ![]() aeh
aeh ![]()
![]() ea sic est
ea sic est ![]() agt
agt ![]()
![]() ag propter figurarum similitudinem. // Ergo ex aequali, sicut
ag propter figurarum similitudinem. // Ergo ex aequali, sicut ![]() zed
zed ![]()
![]() ea sic
ea sic ![]() bg
bg ![]()
![]() ag.
91
// Quod fuit demonstrandum.
ag.
91
// Quod fuit demonstrandum.
Idem ostendam146, si pro tangente btg sumpfero ei parallelum nrp. // Et pro puncto g punctum p et pro t ***147 r quae tangit contrapositam sectionem: concludam enim, quod sicut ![]() np
np ![]()
![]() pa sic iam
pa sic iam ![]() zed
zed ![]()
![]() ea.
92
Sicut proponitur.
ea.
92
Sicut proponitur.