19^a Si contrapositas duae lineae tangentes coincidant: ducantur autem aequidistantes tangentibus invicem secantes et sectionem erit¹⁴⁸ ut tangentium quadrata ad invicem, sic contentum sub iis, quae sunt inter sectionem et coincidentiam ductarum, ad contentum sub similiter acceptis lineis.

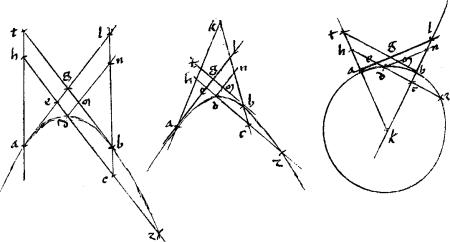
93 Sint contrapositae, quarum diametri aeg, bed. // Centrumque e. // Tangentes az, zd. // Quibus aequidistantes ducantur, hoc est penes az linea hticl¹⁴⁹ et penes dz linea mnxol secantes quidem diametros apud t, c, o, n periferias autem sectionum apud h, i, x, m. // Dico iam [A:73r] quod est, ut az zd sic et hli mlx. 94 // Ducantur enim penes az ipsa xr. // Et penes dz ipsa ip. // Secentque diametri ipsas tangentes apud k, s. // Et quoniam per 47^am primi Conicorum ipsae ht tl¹⁵⁰ sunt aequales. // Ideo, per 6^am secundi Euclidis erunt hli ti simul aequalia tl. 95 // Quare quoniam sicut tl tlo totum scilicet ad totum, sic ti tip ablatum ad ablatum, propter similitudunem figurarum. // Erit per 19^am quinti Euclidis hli ipol reliquum ad reliquum, sicut tl tlo totum ad totum. // Et adhuc, propter figurarum similitudinem, sicut tl tlo sic az azs. 96 // Sed per 4^am huius azs aequale est dkz. // Et per 7^am huius, ipol aequum est crxl. // Igitur sicut az dkz sic hli crxl. // Verum, sicut iam ostensum est, az azs esse, sicut hli ipol sic ostendetur, quod dz dkz est, sicut mlx [S:98] crxl. 97 // Et conversim, sicut dkz dz sic crxl mlx. // Ergo ex aequali, erit, sicut az zd sic hli mlx. // Quod iam proponebatur demonstrandum.

Propositiones Duae Additae

98 Si tangens hyperbolen occurrat secundae diametro: perque occursum agatur parallelus primae diametro incidens periferiae: et per incidentia quaedam penes tangentem producatur; factum trigonum ab acta et producta ad secundam diametrum aequale erit trigono, quod tangens cum coniungente tactum centrumque facit ad eandem¹⁵¹ actam.

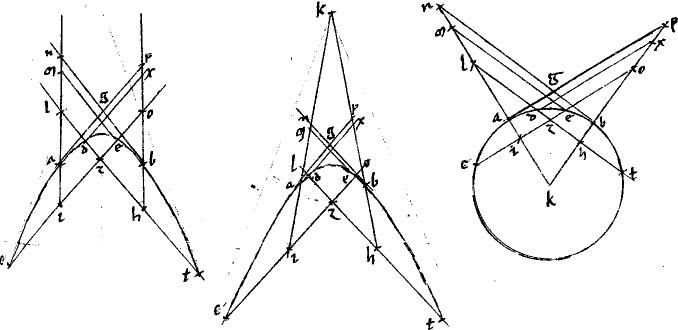
99 Sit hyperbole abgp¹⁵². // Cuius centrum t. // Prima diameter amt. // Secunda zdtle. // Tangens sectionem gml. // Linea klp parallelus ipsi amt diametro. // Linea bxpe aequidistans ipsi gml tangenti. // Per tactum, centrumque ipsa ktgx. // Dico iam quod elp aequale est ^lo klg. // Ducantur enim penes amt diametrum ipsa gd¹⁵³ et ipsa zb ipsi ktgx occurrens apud h. [A:73v] 100 // Quibus peractis, erit iam, per 45^am primi Conicorum bez aequale htz, lgt pariter acceptis. // Quare, ablatis utrinque zbxt et lgt supererunt bxh et lgxe invicem aequalia. // Sed pxk aequum est bxh quandoquidem similia sunt, et latera bx, xp aequalia, per 47 primi Conicorum. // Igitur pxk aequum est ipsi lgxe. 101 // Commune auferatur ipsum lgxp et supererunt ^lum klg et elp aequalia: sicut proponitur demonstrandum. // Idem facilius ostendi potest, ex prima descriptione hyperboles in 45^a primi Conicorum, si supponatur ibi linea hzb transira per punctum l. // Sic enim bel aequum arguetur hlt et lgt hoc est¹⁵⁴ toti hlg. // Quod est cum eo, quod hic proponitur.

102 Si tangens hyperbolen occurrat secundae diametro: perque extremum primae diametri ducatur parallelus tangenti; contentum triangulum sub parallelo diametrisque aequale erit trigono, quod tangens cum coniungente tactum centrumque facit ad secundam diametrum.

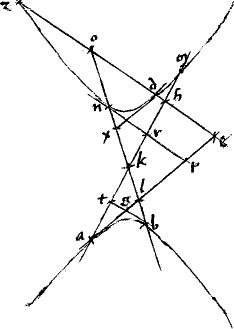
103 Sit hyperbole agb. // Cuius centrum t. // Prima diameter amt. // Secunda zdtle. // Tangens sectionem gml. // Linea tgh per tactum centrumque ipsi¹⁵⁵ zbh penes [A:74r] amt diametrum ductae occurrens apud h. // Et dg penes at. // Dico iam quod ate aequale est ^lo gtl. 104 // Namque, ut in praemissa, erit per 45^am primi Conicorum, bez aequale htz lgt simul sumptis. // Quare, ablatis utrinque zbxt et lgt relinquetur bxh aequum lgxe. // Sed axt aequale iam¹⁵⁶ bxh quoniam similia sunt; et eorum latera bx xa inter se aequalia, per 47^am primi Conicorum. 105 // Igitur axt aequum erit ipsi lgxe. // Commune aufera[S:99]tur mgxa. // Et supererit mgt aequum lmae. // Commune apponatur ltm. // Et conflabitur lgt aequale iam ^lo eat. // Quod proponebatur demonstrandum. 106 // Nec potest praesens ostendi ex secunda huius, ex aequalitate scilicet mgt et lmae non enim tribui potest huic casui secundae demonstratio, quippe quae pendet ex demonstratione 45^ae primi, in qua gtm quod videlicet lmae aequale arguitur, nunquam ibi sistitur ad t centrum sed nunc supra illud, nunc sub eo. // Itaque hic modus necessarius erat ad id, quod hic proponitur demonstrandum. 107 Et manifestum est, quod sicut est et tl basis videlicet ad basim: sic est dg ta altitudo scilicet ad altitudinem: namque trigonorum aequalium bases sunt fastigiis reciprocae.