75 [A:71v] 16^a Si coni sectionem, vel circuli periferiam duae lineae tangentes coincidant a quodam vero puncto eorum, quae sunt in sectionem ducatur linea penes quamdam tangentium secans sectionem et alteram tangentium¹²¹: erit ut quae fiunt a tangentibus tetragona ad invicem, sic contenta superficies sub tota ducta et sui parte, quae est inter sectionem et tangentem, ad id, quod fit ex recepta ad tactum tetragonum¹²².

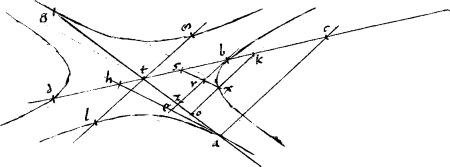
76 Sit coni sectio, vel circuli periferia ab. // Quam tangant lineae ag, gb. // Et per quoddam¹²³ relictum in sectione punctum d ducatur penes bg tangentem ipsa edz. // Dico iam quod sicut est bg ag sic est zed ea. // Ducantur enim per a, b diametri aht, bcl. 77 // Per d autem dmn aequidistans ipsi ag. // Eritque per 47^am et 46^am primi Conicorum dc aequalis cz. // Quare, per 6^am secundi Euclidis zed cum cd aequum est ce. // Sed ec cd sicut¹²⁴ ecl cdn utraque enim ratio dupla rationis laterum in similibus figuris. // Et permutatim, sicut ec ecl totum scilicet ad totum, sic cd cdn ablatum ad ablatum. 78 // Et ideo, per 19^am quinti Euclidis zed dl reliquum ad reliquum, sicut ec ecl totum scilicet ad totum. // Item ec gb sicut ecl gbl propter similitudinem figurarum. // Et permutatim sicut ec ecl sic gb gbl. // Igitur sicut zed dl sic gb gbl. 79 // Sed dl aequum ^lo125 aeh per 2^am huius, et per primam, gbl aequum gat. // Ergo sicut¹²⁶ zed aeh sic gb gat. // Et permutatim zed gb sicut¹²⁷ aeh gat hoc est sicut ea ag utrobique enim ratio dupla¹²⁸ laterum rationis¹²⁹. // Et rursus permutatim, ut zed ea sic bg ag. 80 // Quod fuit demonstrandum. [A:72r]