[A:70v] 15^a Si in una contrapositarum ad coniunctionem lineae tangentes coincidant: et per tactus diametri ducantur: relictumque sit quoddam¹⁰² punctum in utravis coniunctarum lateralium: et ab ipso aequidistantes ducantur tangentibus usque ad diametros; factum sub ipsis ad sectionem trigonum, facto trigono ad centrum maius est trigono basis habente tangentem, summitatem vero centrum contrapositarum.

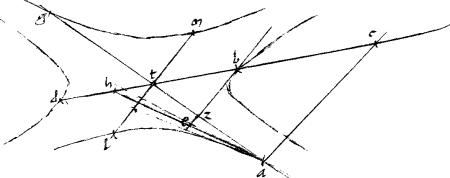
61 Sint ad coniunctionem contrapositae ab, hs, k, x. // Quarum centrum t. // Et sectionem ab tangant ade, bdg. // Et per a, b tactus ducantur diametri agtz beytlk¹⁰³. // Et relictum sit in sectione hs punctum quoddam¹⁰⁴ s per quod ducantur penes bg quidem ipsa szl penes ae ipsa sy hoc est duae lineae tangentibus paralleli. // Dico iam quod sly aequale est tlz, tgb¹⁰⁵ pariter acceptis. 62 // Ducatur¹⁰⁶ enim per t penes bg ipsa xth. // Penes autem ae ipsa hic occurrens ipsi ag apud c. // Item [S:94] penes bt ipsa so. // Quibus peractis, manifestum est, per 20^am 2ⁱ Conicorum, quod xth, btk coniugatae sunt diametri quodque so aequidistans ipsi bk applicata est ordinate ipsi xtho quodque parallelogrammum est ipsum slto. 63 // Quoniam igitur tangit¹⁰⁷ bg et¹⁰⁸ per tactum¹⁰⁹ est bt et altera tangens est ae. // Fiat iam ut db be sic mn duplam ipsius bg. // Eritque per 50^am primi Conicorum, ipsa mn recta speciei ad diametrum bk. // Secetur ergo per medium mn apud p. 64 // Eritque ut bd be sic mp bg. // Fiat utique ut xh kb sic kb R. // Eritque, per ultimam primi Conicorum, ipsa R recta speciei ad xh diametrum. // Quoniam autem per primam sexti Euclidis est ut db be sic db dbe. Itemque, sicut mp bg sic mp, bt gbt. // Erit iam sicut db dbe sic mp bt gbt. // 65 Aequale autem est mp bt ^to th quandoquidem, per ultimam primi Conicorum kb mn aequale est ^to xh atque mp bt quadrans est ipsius kb mn ipsumque th quadrans ipsius xh quoniam videlicet latera laterum¹¹⁰ dimidia. // Igitur erit, sicut db dbe sic th gbt. // 66 Et permutatim ut db th sic dbe gbt. Et sic dbe hti quandoquidem propter aequidistantiam laterum sunt similia et perinde ut db th per 17^am et 18^am 6ⁱ. // Sed¹¹¹ sicut dbe gbt sic dbe gbt quoniam utraque ratio compasita est ex rationibus eorumdem laterum per 24^am 6ⁱ Euclidis. 67 // Itaque dbe quam rationem ad hti eandem habet ad gbt. // Quare, per 9^am quinti gbt hti sunt ad invicem aequalia. // Cum autem, ratio tb gb componatur ex rationibus tb mp atque mp gb sitque sicut tb mp sic kb mn utraque enim dupla¹¹² : et ideo sicut R xh per ultimam primi Conicorum atque fuerit,ut mp gb sic db be. 68 // Propterea et ratio tb gb componetur ex rationibus R xh atque db be. // Sed sicut [A:71r] tb gb sic tl lz propter triangulorum similitudinem. // Ergo et ratio tl, // lz componetur ex rationibus iisdem, scilicet R xh atque db be. // Sed propter linearum aequidistantiam, sicut db be sic ht ti. // Ergo ratio tl lz componetur ex rationibus R xh atque ht ti. 69 // Aequalis autem est in parallelogrammo slto ipsa so ipsi lt. // Quare et ratio so lz componetur ex rationibus R xh atque ht ti. // Estque so applicata diametro transversae xh et eius rectum latus R et ipsa ht semidiameter transversa. // 70 Propterea, per 41^am primi Conicorum, species, quae fit ex to vel ex ei aequali ls similis speciei factae ex th aequalis erit speciebus duabus [[similis]]¹¹³ ipsi scilicet factae ex th factaeque¹¹⁴ ex so vel ex ipsius aequali lt quae videlicet sit aequiangula ipsi factae ex th. 71 // Quod cum verum fit de parallelogrammis, verum erit et de triangulis parallelogrammorum dimidiis sicut in 43^am primi Conicorum ostensum fuit. // Quam ob rem lsy aequale erit duobus ^lis scilicet ^lo thi sibi¹¹⁵ iam simili et tlz quod in uno tantum angulo apud l illis aequiangulum est. 72 // Sic enim sequitur, ut hoc et utrumlibet illorum dimidia sint parallelogrammorum aequiangulorum: et illa duo scilicet lsy, thi dimidia sint non solum aequiangulorum sed et similium parallelogrammorum¹¹⁶. // Verum gbt ostensum fuit aequale ^lo hti. // Igitur et lsy aequum erit gbt, tlz. // Quod fuit demonstrandum. 73 Et manifestum¹¹⁷ fuit, quod quoniam¹¹⁸ lsy aequale est thi, tlz [[decepto]] communi tlz restat sytz aequale thi. // Rursumque ablato communi tqy supersunt duo quadrilatera sztq, qhiy invicem aequalia, terminata quodlibet¹¹⁹ ad duas diametros atz, ktb ad quas permutatim applicata sunt trapeziorum latera aequidistantia.

[S:95] Scholium

74 Quoniam, ut patuit, linea mn sit¹²⁰ recta ad transversam ktb. // Nec non linea R recta ad transversam xth. // Iam, per ultimam primi Conicorum, erunt ipsae mn xth ktb R in proportione continua: unde pendet tota demonstratio, quod gbt, hti sunt invicem aequalia.