[A:70r] 14^a Iisdem subiectis, si in una sectionum punctum quoddam⁹⁶ relictum sit: et ab ipso aequidistantes ducantur tangentibus usque ad diametros; factum ad centrum trigonum, facto circa eumdem angulum triangulo differt trigono basim habente tangentem, summitatem vero centrum.

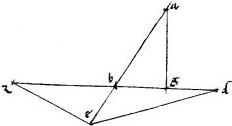
55 Sint alia quidem eadem. // Relictum autem sit in sectione b quoddam⁹⁷ punctum x. // Et per ipsum penes ah tangentem ducatur xrs. // Penes be vero tangentem xok. // Dico iam quod otk differt a xsk in ipso tbz. // Ducatur enim penes ipsam be ipsamque oxk linea ipsa ac. // Quoniam igitur, per eadem, quae prius, sectionum al, gm diameter est ltm. // 56 Coniugata autem ei⁹⁸ diameter dtb per 20^am 2ⁱ Conicorum cui occurrit ah tangens: et cui applicata ordinate est ac. // Ideo iam, per 40^am primi Conicorum: ratio ac ch componetur ex rationibus tc ca atque⁹⁹ lm rectum speciei latus. // Sed ut ac ch sic xk ks. // Ut autem tc ca sic tk ko et tb bz propter triangulorum similitudinem. 57 // Item per ultimam primi Conicorum, sicut lm transversa diameter ad rectum speciei latus: sic rectum¹⁰⁰ ad db coniugatam diametrum. // Igitur et ratio xk ks componetur ex rationibus tb bz id est tk ko et recti lateris db diametrum. 58 // Quare per 41^am primi Conicorum, species, quae fit ex tk similis speciei factae ex tb aequalis est speciebus duabus, ipsi videlicet factae ex tb ipsique factae ex xk quae scilicet sit¹⁰¹ aequiangula ipsi factae ex tb. // Quod cum intelligatur de speciebus parallelogrammis iam et ad triangula quae sunt parallelogrammorum dimidia referri potest, sicut in 43^a primi Conicorum demonstratum est. // 59 Itaque otk aequale erit duobus triangulis videlicet ^lo ztb sibi simili, atque ^lo xsk quod scilicet in uno angulo tantum illis aequiangulum est: sic enim sequitur ut hoc et utrumlibet illorum dimidium sit parallelogrammorum aequiangulorum. // Ergo otk differt a ^lo xsk in ipso tbz ^lo. 60 // Quod fuit demonstrandum.