Lemma

Si duorum triangulorum duo anguli sint aequales duobus rectis: et angulos continentia latera reciproca; aequalia sunt triangula.

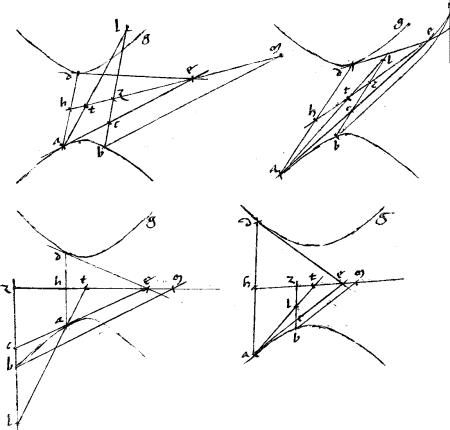
Triangula abg dbe habeant angulos ad b duobus rectis aequales. 48 // Sitque sicut ab be sic db bg. // Aio iam quod aequalia sunt abg dbe ^la. // Sit enim sicut ab be et perinde sicut db bg sic bz bg producta videlicet in rectum gb. // Et connectatur ze. // Eritque per 9^am quinti Euclidis bz aequalis ipsi db. // Quare per 38^am91 primi eiusdem deb bze aequalia. // 49 Sed abg bze per 14^am 6ⁱ eiusdem aequalia⁹²: quandoquidem circum angulos ad b aequales [A:69v] latera sunt reciproca. // Igitur abg dbe sunt aequalia: quod est propositum.

13^a Si in contrapositis ad coniunctionem, lineae continuatim sectiones tangentes coincidant: et per tactus diametri ducantur; aequalia erunt trigona, quorum communis summitas est centrum contrapositarum.

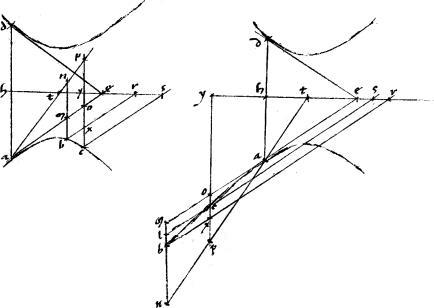
50 Sint coniunctae contrapositae, in quibus a, b, g, d puncta. // Ipsasque a, b sectiones collaterales, utramque videlicet ab uno latere, utpote a dextris⁹³ tangant be, ae concurrentes ad e. // Sitque centrum t. // Et coniunctae at, bt producantur ad gd in oppositas sectiones. // Secetque at diameter ipsas be tangentem in puncto z. 51 Et⁹⁴ ae producta occurrat ipsi dt apud h. // Dico iam quod aequale est bzt ^lo ath. // Ducantur enim per a, t puncta penes be tangentem ipsae ltm ad sectiones a, g atque ac ipsi db productae occurrens apud c punctum. // Quoniam igitur bze tangit sectionem b et per tactum diameter dtb ipsique be aequidistat ltm iam ipsae ltm, ac ordinatae sunt ad db diametrum, quandoquidem ad eamdem ordinata est be tangens per additam 32^ae primi Conicorum. 52 // Atque, per 16^am eiusdem et per 20^am 2^{i 95} , ipsa ltm coniugata diameter est ipsi dtb diametro. // Cumque talium diametrorum utraque possit speciem alterius per conversionem ultimae primi Conicorum ipsaque ah tangens sectionem a occurrat eius secundae diametro apud h. // Propterea per 38^am primi Conicorum [S:93] cth equum erit ^to bt. // 53 Quare per 16^am sexti Euclidis sicut ct th sic tb ht. // Per 2^am autem 6ⁱ Euclidis sicut ct tb sic at tz. // Igitur sicut est at tz sic bt th suntque ^lorum btz, ath anguli btz, ath per 13^am primi Euclidis duobus rectis aequales. // Itaque talium triangulorum latera continentia aequales duobus rectis angulos reciproca sunt. 54 // Atque ideo per praemissum lemma ipsa btz ath ad invicem aequalia sunt. // Quod erat demonstrandum.