51^a Data coni sectione, ducere tangentem, quae ad ductam diametrum per punctum tactus aequalem angulum contineat dato acuto.

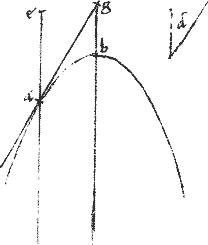
Sit coni sectio primum parabole ab. // Cuius axis vel diameter bg³⁹⁰. // Datus d angulus³⁹¹.

// Oportet utique ducere tangentem, quae cum diametro ducta per punctum tactus angulum contineat aequalem angulo d. // Ducatur per praemissam, tangens ag faciens cum axi bg angulum agb aequalem angulo d.

[A:59r] Et per punctum tactus a ducatur ea parallelus ipsi bg. // Quae per 46^am praemissi diameter erit faciens angulum eag ipsi angulo agb coalterno coalterno³⁹² et perinde ipsi d angulo dato aequalem: sicut proponitur.

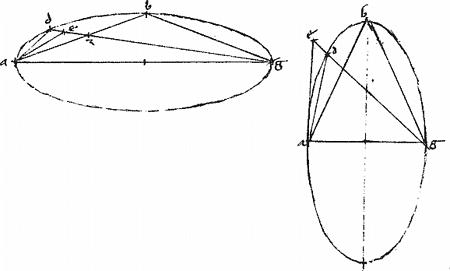
Sit deinde hyperbole ab. // Cuius centrum g. // non tangentes³⁹³ egz. // Datus angulus d et reliqua.

// Exponatur quaedam linea hk super quam costituitur³⁹⁴ circuli portio htk³⁹⁵ suscipiens angulum aequalem angulo egz per 31^am 3ⁱⁱ Euclidis. // Et hk per medium divisa in puncto l ponatur ipsi d angulo aequalis angulus klt. // Et coniungantur ht tk. // Quibus peractis, ponatur ipsi htl angulo [S:78] aequalis angulus ega. // Coincidet autem ga sectioni, per 2^am huius: coincidat apud a. // Et fiat ipsi d angulo sive ipsi klt aequalis angulus gaz et ducatur za donec ipsi ge occurrat apud e. // Erit enim agz ipsi ltk aequiangulum: itemque age ipsi lth aequiangulum: totumque egz toti htk aequiangulum: // quare per 4^am Sexti Euclidis latera lateribus proportionalia. // Itaque cum hl lk³⁹⁶ sint aequales, erunt et ea az inter se aequales. // Igitur, per 9^am huius, eaz tanget sectionem apud a faciens angulum gaz ipsi angulo d aequalem. Sicut faciendum proponitur.

SCHOLIUM

Superest nunc idem problema in data ellipsi absolvere. Sed quoniam, in ellipsi non ad omnem datum acutum angulum licet ducere diametrum ad tangentem³⁹⁷, quemadmodum in parabola, et hyperbola licebat; propterea ad determinandum angulum acutum minimum, ad quem in proposita ellipsi diameter incidit hoc est incidere potest tangenti, praemittenda sunt lemmata quaedam quae quidem non solum tanquam praeambula, sed etiam ut theoremata et necessaria et iucunda scitu venient³⁹⁸.

1. Circulus, cuius diameter est minor axium ellipseos, totus intra sectionem cadit.

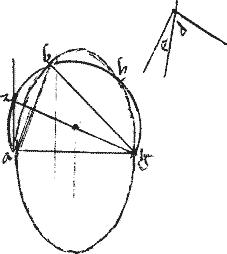
Sit ellipsis ab. // Cuius minor axis sit bg. // Super quo quasi diametro circulus describatur dbg³⁹⁹.

// Dico iam quod circulus dbg totus cadit intra ellipsim. // Sit enim recta, ad⁴⁰⁰ possunt ordinatae [A:59v] ad bg ipsa be ad rectos ipsi bg. // Et coniungatur eg.// Eritque per 13^am401 be maior quam bg. // Quandoquidem maior axis est medius proportionalis inter gb be. // Capiatur itaque quodvis punctum in periferia circuli, quod sit d per quod ordinate ducatur adzh secans ellipsim apud a axim apud z ipsamque ge apud h⁴⁰².

// Eritque maior zh quam zg quoniam be maior quam bg. // Quare, cum per 13^am praecedentis az possit bzh atque per 34^am 3ⁱⁱ Euclidis dz possit bzg. // Iam longior⁴⁰³ az quam dz et perinde, punctum d intra ellipsim cadit.

// Et similiter ostendam quod omnia puncta et ideo tota periferia circuli cadit intra ellipsim demptis solum punctis b g contactuum. // Quod erat demonstrandum.

2. Circulus, cuius diameter est maior axium ellipseos, totus extra sectionem cadit.

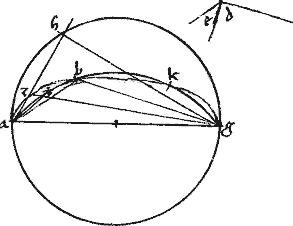
Sit ellipsis ab. // Cuius maior axis bg. // Super quo quasi diametro circulus describatur dbg. // Dico iam quod circulus dbg totus cadit extra ellipsim.

// Sit enim recta, ad quam possunt⁴⁰⁴ ordinatae ad axis bg ipsa be ad rectos ipsi bg.

Et coniungatur eg. // [S:79]Eritque, per 13^am praemissi be minor, quam bg. // Quandoquidem minor axis est medius proportionalis inter gb be. // Capiatur itaque quodvis punctum in periferia circuli, quod sit d per quod ordinate ducatur dazh secans ellipsim apud a axim apud z ipsamque eg apud h.

// Eritque minor zh quam zg quoniam be minor quam bg. // Quare cum per 13^am praecedentis az possit bzh atque per 34^am 3ⁱⁱ Euclidis dz possit bzg iam brevior erit az quam dz et perinde punctum d extra ellipsim cadit. // Et similiter ostendam quod omnia puncta periferiae circularis⁴⁰⁵ et ideo tota periferia circuli cadet extra sectionem exceptis solum punctis b g contactuum.

Quod fuit demonstrandum.

3. Angulus supra minorem axium ellipsis ad periferiam constitutus acutus est.

Sit ellipsis abg. // Cuius minor axis ag. // Angulus ad periferiam abg. Dico iam quod acutus est angulus abg. //

[A:60r]

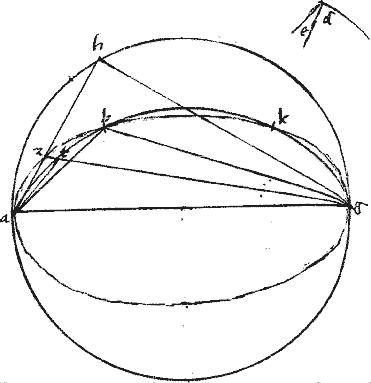
// Nam, per antepraemissum lemma, circulus, cuius diameter ag cadit intra sectionem. // Secabit ergo periferia circuli utramque linearum ab bg. // Secet ipsam bg in puncto d et connectatur ad. // Eritque per 29^am 3ⁱⁱ Euclidis adg angulus rectus: qui cum maior sit angulo abg sibi intrinsecus opposito: erit iam ipsae abg acutus: quod erat demonstrandum.

4. Angulus supra maiorem axium ellipsis ad periferiam positus obtusus est.

Sit ellipsis ab⁴⁰⁶ g cuius maior axium ag. // Angulus ad periferiam ab⁴⁰⁷ g. // Dico iam quod obtusus est angulus ab⁴⁰⁸ g.

// Siquidem per 2^um praemissorum lemmatum circulus, cuius diameter ag cadit extra sectionem. // Igitur utravis linearum ab⁴⁰⁹ b⁴¹⁰g producta incidet circulo extra sectionem.

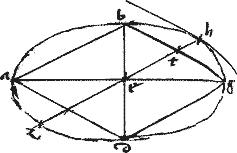
// Incidat gb⁴¹¹ producta circulo apud d⁴¹² et coniungatur ad⁴¹³. // Eritque per 29^am 3ⁱⁱ Euclidis ad⁴¹⁴g angulus rectus: quo cum maior sit angulus ab⁴¹⁵g extrinsecus: iam ipsae ab⁴¹⁶g obtusus erit.

// Quod est demonstrandum.

5. In triangulo rectilineo ductae lineae penes minus laterum includunt de maiori maius spatium eo, quo differunt: actae vero penes maius laterum intercipiunt de minori minus eo, quo differunt, hoc est, quo longior acta excedit breviorem.

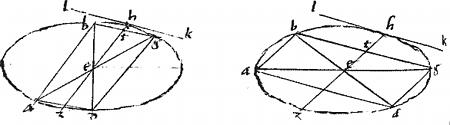
Sit triangulum abg. // Cuius ab latus minus sit bg latere. // Ductae autem penes ipsum ab sunt⁴¹⁷ de⁴¹⁸ zh. // Ductae vero penes ipsum bg sint zk dt. // Secet autem de ipsam zk apud l⁴¹⁹.

// Unde patet quod dlz simile est abg. // Et ideo, sicut ab minus⁴²⁰ quam bg ita dl minus quam lz. // Sed lz aequalis ipsi e⁴²¹ h. // Igitur eh maius quam dl⁴²². // Quod est primum ex propositis.

// Et quoniam dl aequalis⁴²³ ipsi tk. // Ideo tk minus quam lz.// Quod est reliquum ex iis⁴²⁴, quae demonstranda proponuntur.

[A:60v] [S:80] 6. Circulus in ellipsi per axis minoris extrema et verticem ductus secat ellipsim in ipsis extremis et in ipso vertice tangit, inceditque a tactu ad sectiones extra ellipsim, deinceps intra ellipsim.

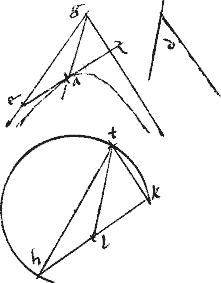
Sit ellipsis abg. // Cuius axes ag minor: bd⁴²⁵ maior se invicem secantes apud e. // Circulus autem describatur incedens per puncta a b g qui sit abgz.

// Dico iam quod circulus abgz secat ellipsim apud a g puncta: tangitque apud b. // Quodque periferia abg incedit⁴²⁶ extra ellipsim: residua vero azg intra ellipsim.

// Sit enim recta, ad quam possunt ordinatae ad diametrum bd ipsa bh et connectatur dh. // Eritque bh minor quam bd quandoquidem ag minor axis est medius proportionalis inter db bh. // Deinde capiatur in periferia circulari abg punctum quodvis, utpote t et ordinata ducatur ad diametrum bd linea tklm secans ellipsim quidem apud k axim bd apud l ipsamque hd apud m. // Ipsa autem dh secet axim ag apud n. // Iamque per praemissum lemma, erit erit⁴²⁷ excessus lm super en minor quam linea le. // Sed en aequalis ez cum per 34^am 3ⁱⁱ Euclidis ae possit b⁴²⁸ ez et per 13^am praemissi, eadem ae possit ben. // Igitur lz maior⁴²⁹, quam lm. // Verum per 34^am 3ⁱⁱ Euclidis tl potest b⁴³⁰lz et per 13^am praemissi kl potest blm.

// Ergo tl⁴³¹ longior⁴³² quam kl. // Quare punctum periferiae circularis t est extra ellipsim. // Et similiter ostendam quod omnia puncta circularis periferiae abg et perinde tota periferia est extra ellipsim excepto puncto b contactus.

// Non aliter ostendam quod periferia azg intra ellipsim cadit. // Quodvis⁴³³ utrumque manifestum sit ex conditione ellipticae, ac circularis portionis proportionis⁴³⁴ // Quod quidem fuerat demonstrandum.

7. Circulus in ellipsi per axis maioris extrema, et verticem descriptus secat ellipsim in ipsis extremis: tangit autem in ipso vertice: inceditque a tactu ad sectiones intra ellipsim, deinceps extra.

Sit ellipsis abg⁴³⁵ .// Cuius axes ag maior bd minor se vicissim secantes apud e. // Circulus autem describatur incedens per puncta a b g hucusque praeter figuras [[Ta?]] 27 [[Mai]] 1547⁴³⁶ qui sit abgz.

// Dico iam quod circulus [A:61r] abgz secat ellipsim apud a g puncta: tangitque apud b. // Quodque periferia circuli abg incedit intra ellipsim: residua vero azg extra ellipsim⁴³⁷.

// Sit enim recta, ad quam possunt ordinatae ad transversam bd sive axim, ipsa bh et connectatur dh. // Eritque bh maior quam bd quandoquidem ag maior axis est medius proportionalis inter db bh.

// Deinde capiatur in periferia circulari abg punctum quodvis utpote t et ordinate ducatur ad diametrum bd linea ktlm⁴³⁸ secans ellipsim quidem⁴³⁹ apud k axim autem bd apud l ipsamque hd apud m.

// Ipsa autem dh secet axim ag productum apud n.

// Iamque per antepraemissum lemma, excessus lm super en maior⁴⁴⁰ quam linea le. // Sed en aequalis ez cum per 34^am 3ⁱⁱ Euclidis ae possit bez et per 13^am praemissi, eadem ae possit ben.

// Igitur lz minor⁴⁴¹, quam lm. // Verum per 34^am 3ⁱⁱ Eu[S:81]clidis tl potest blz et per 13^am praemissi kl potest blm.

// Ergo tl brevior⁴⁴², quam kl. // Quare punctum periferiae circularis t est intra ellipsim. // Et similiter ostendam quod omnia puncta circularis periferiae abg et perinde ipsa periferia tota est intra ellipsim excepto puncto b contactus. // Nec secus demonstrabo quod periferia residua azg extra ellipsim cadit. // Quamvis utrumque manifestum sit ex conditione figurarum. // Quod erat demonstrandum.

8. Angulorum in ellipsi supra minorem axium constitutorum ad periferiam minimus est, qui ad verticem sectionis.

Sit ellipsis abg cuius minor axis ag. // Vertex, hoc est extremum maioris axis sit b. // Angulus abg ad verticem. // Et angulus adg ad aliud quodvis periferiae punctum, positus. // Dico quod minor est angulus abg angulo adg.

// Nam per antepraemissum lemma, circularis periferia, quae [A:61v] per puncta a b g describitur, cadit extra ellipsim, excepto puncto tactus b.

// Igitur gd producta incidet circulo extra ellipsim: // incidat ad punctum e et coniungatur ae. // Eruntque, per 20^am 3ⁱⁱ Euclidis anguli abg aeg aequales in eadem videlicet circuli portione constituti. // Verum angulus adg maior⁴⁴³ angulo aeg sibi intrinsecus opposito. // Ergo et idem adg angulus maior angulo abg verticali. // Cum autem anguli quicumque ad periferiam abd positi non sint iam⁴⁴⁴ in periferia circularis portionis sed ellipticae, omnino different⁴⁴⁵ inter se. // Quare et ipse angulus verticalis et minor unoquoque reliquorum, et omnium minimus dicetur.

// Quod erat demonstrandum.

9. Angulorum in ellipsi supra maiorem axium ad periferiam positorum maximus est, qui ad verticem sectionis.

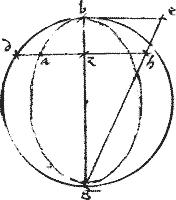
Sit ellipsis abg. // Cuius maior axis ag. // Vertex hoc est extremum minoris axis b. // Angulus abg ad verticem. // Et angulus adg ad quodvis relictum periferiae punctum positus.

// Dico iam, quod maior est angulus abg ipso adg angulo.

// Nam, per antepraemissum lemma, circularis periferia, quae per puncta a b g deducitur, cadit intra ellipsim, excepto ipso tactus puncto b. // Igitur circulus incidet ipsi gd apud aliquod punctum in segmento dz. // Incidat ad e punctum. // Et coniungatur ae. // Eruntque, per 20^am 3ⁱⁱ Euclidis anguli abg aeg invicem aequales in eadem scilicet circuli portione positi.

// Sed angulus aeg maior angulo ab⁴⁴⁶ g intrinseco. // Ergo et abg abg⁴⁴⁷ maior erit eodem adg angulo.

// Cum autem anguli quilibet ad periferiam adb positi inter se differant, quandoquidem non in circularis sed elliptica portione sunt positi. // Iam ipse angulus verticalis est maior unoquoque reliquorum et maximus omnium erit.

// Quod erat demonstrandum.

[A:62r] 10. In data ellipsi supra minorem axim angulum dato acuto aequalem ad periferiam constituere. // Oportet utique datum angulum acutum non esse minorem angulo verticali.

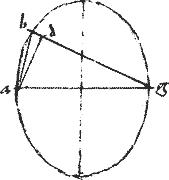
Sit data ellipsis abg. // Cuius axis minor sit ag. // Datus angulus acutus d.

// Oportet supra axem ag ad periferiam ellipsis angulum angulo d aequalem constituere. // Necesse est autem angulum d angulo verticali supra ag axim ad verticem posito [S:82] non esse minorem. // Secus enim problema esset impossibile, per antepraemissum lemma, quandoquidem angulo verticali in ellipsi supra minorem axim posito minor non datur.

// Sit itaque totalis angulus ed rectus: hoc est, ut datus acutus d una cum angulo e rectum angulum conficiat. // Et a puncto a ipsi ag ad rectos excitetur az indefinita: cui occurrat ipsa gz faciens scilicet angulum agz aequalem angulo e. // Et quoniam anguli agz azg conficiunt rectum: et ipse ed totalis rectus. Demptis iam utrinque angulis agz et e supersunt anguli azg et d invicem aequales. // Deducatur itaque, per 5^am 4ⁱ Euclidis, circulus circa triangulum azg⁴⁴⁸. // Qui omnino secabit periferiam ellipsis cum punctum z sit extra periferiam ellipsis per 17^am praemissi: et angulus azg sit maior angulo verticali. Secet in punctis bh. // Quorum alterum coniungatur cum ag⁴⁴⁹ punctis: // eritque per 20^am 3ⁱⁱ Euclidis angulus abg aequalis angulo azg et perinde angulo d et supra axim minorem ellipsis ad periferiam positus. // Quod faciendum proponebatur.

11. In data ellipsi supra maiorem axim angulum dato obtuso aequalem ad periferiam constituere.

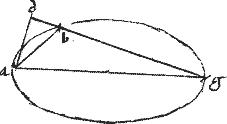
// Oportet utique datum angulum obtusum non esse maiorem angulo verticali.

Sit data ellipsis abg. // Cuius axis maior sit ag. // Datus angulus obtusus ed totalis, ita ut d sit rectus. // Oportet super axim ag angulum angulo ed aequalem ad periferiam ellipsis costituere. // Necesse est autem angulum ed angulo verticali supra ag axim ad verticem posito non esse minorem⁴⁵⁰: secus enim problema esset impossibile, quandoquidem, per antepraemissum lemma, [A:62v] angulo verticali, in ellipsi supra maiorem axim posito maior⁴⁵¹ non datur in periferia.

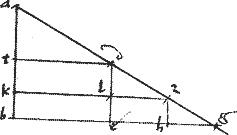
// Sit ergo circulus, cuius diameter ag qui⁴⁵² per 2^um horum lemmatum, extra ellipsim cadit, qui⁴⁵³ sit ahg. // Ponaturque angulus agh ipsi angulo e aequalis.

// Et connectatur ah quae, per 32^am praemissi, secabit periferiam ellipsis: secet in puncto z et connectatur gz. // Eritque angulus azg aequalis duobus intrinsecis, angulo scilicet ahg recto, et angulo hgz et perinde minor erit angulo totali ed qui constat ex d recto et ex angulo e qui est aequalis ipsi agh minor inquam in angulo agz.

// Fiat itaque ipsi angulo agz aequalis angulus zat ut scilicet at apud t punctum ipsi zg coincidat. // Eritque angulus atg maior angulo azg intrinseco in angulo zat.

// Et tantumdem maior fuit angulus totalis ed ipso eodem angulo azg hoc est in angulo agz. // Aequalis ergo erit angulus ed datus angulo atg.

// Describatur igitur, per 5^am 4ⁱ Euclidis circa atg circulus, qui omnino secabit periferiam ellipsis, cum angulus verticalis sit maior angulo atg et perinde intra periferiam circuli cadat⁴⁵⁴.

// Secet itaque periferiam circuli, per a t g puncta incedens⁴⁵⁵ periferiam⁴⁵⁶ ellipsis apud b k puncta. // Quarum alterum b coniungatur cum a g punctis.

// Eritque, per 20^am 3ⁱⁱ angulus abg angulo atg et ideo ipsi angulo ed totali dato aequalis, et super axim maiorem ag ad periferiam ellipsis positus. // Quod faciendum proponebatur.

SCHOLIUM

Notandum quod in praemissa, circulus descriptus per puncta a b g semper habet centrum in axi maiore ellipsis: in praesenti autem circulus incedens per a t g puncta [S:83] semper habet centrum in axi minore, si opus est, extra producto: et ideo tam in praemissa, quam in praesenti [A:63r] propositione, talis circulis semper secat ellipsim apud quatuor puncta hoc est apud ipsa a g axis extrema et apud alia duo puncta.

// Quod quidem ex ipsa aequalitate linearum et angulorum apud⁴⁵⁷ sectionum puncta in portione circuli constitutorum manifestum est. // Oportet enim circularis portionis periferiam incedere per angulos aequales in elliptica periferia positos et perinde in ipsis angulis ipsam ellipsim secare.

// Unde necesse est in praecedenti, ut periferia circularis azb secet ellipsim apud puncta b h in quibus anguli in ellipsis periferia super axim ag positi sunt aequales. // In praesenti autem propositione, necesse est, ut periferia circularis atb secet ellipsim apud puncta b k in quibus anguli in ellipsis periferia super axim ag constituti sunt aequales.

Quod autem tales anguli sunt⁴⁵⁸ aequales, patet, quoniam ipsa puncta in quibus sunt, aeque remota sunt ab extremis axis ag item quoniam ab ipsis punctis ordinatae ad axim aequalia segmenta hinc et inde abscindunt ex⁴⁵⁹ axi: et ipsae sunt aequales. // Et vice versa ex aequalitate angulorum arguitur aequalitas linearum.

// Unde sicut in praecedenti propositione, angulus super axim ag ag⁴⁶⁰ minorem ad periferiam ellipsis ab positus maior est angulo abg et ipse angulus abg maior angulo verticali: et verticalis omnium minimus: ita in praesenti propositione, angulus azg minor est angulo abg et angulus abg minor angulo verticali: et verticalis omnium maximus.

Unde manifestum est, quod angulorum in ellipsi super minorem axim ad ad⁴⁶¹ periferiam positorum, qui propinquior est verticali, minor est: super axim vero maiorem positorum, vicinior verticali, maior.

// Preaterea notandum quod anguli in ellipsi non super axes, sed super alias diametros ad periferiam constituti possunt esse obtusi, recti, et acuti. Namque deducto semicirculo super diametrum ipsam, angulus super diametrum ad punctum, in quo semicirculus ellipsim secat, positus rectus est per 29^am462 3ⁱⁱ Euclidis unde angulus ad periferiam ellipsis intra semicirculum clausam, obtusus⁴⁶³: ad residuam, quae semicirculum excedit, constitutus, acutus erit.

// Anguli autem in ellipsi neque super axes, neque super diametros, sed super alias ordinate ductas, sive chordas ad⁴⁶⁴ periferiam locati variantur iuxta qualitatem assumptae periferiae.

[A:63v] 12. In ellipsi diameter, aequidistans lineae connectenti axium extrema, est illa, quae omnium diametrorum maxime obliqua incidit tangenti sectionem apud ipsum tactum, suisque ordinate ductis in sectionem.

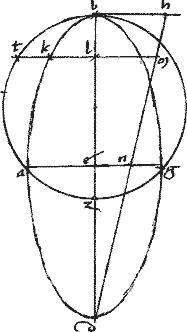
Sit ellipsis abg. // Cuius axes ag bd quorum maior ag quorum maior ag⁴⁶⁵ sese vicissim secantes apud e. // Et⁴⁶⁶ coniuncta ab ducatur ipsi aequidistans diameter zeh.

// Dico iam quod diameter zeh omnium diametrorum obliquissime secat suas ordinatas.

// Agatur enim, per 49^am huius khl tangens sectionem apud h. // Et coniungatur bg secans ipsam eh apud t. // Eritque bg bifariam secta apud t per 2^am 6ⁱ Euclidis.

Cum et aequidistans ipsi ab bifariam secet ag apud e. // Quare per 6^am huius kl tangens aequidistabit ipsi bg et perinde ambae ordinate ductae sunt ad ipsam zh diametrum. // Ostendendum est igitur quod zh maxime inter diametros obliqua incidit ipsis kl bg ordinatis. // Coniunctis enim gd da erunt opposita triangula aequilatera et aequiangula invicem. // Et ob id parallelogrammum erit abgd rhombus scilicet. // Et propter aequidistantiam linearum anguli lht bte iam inter se aequales, singuli aequales erunt et⁴⁶⁷ angulo bgd. // Sed, per 8^um lemmatum⁴⁶⁸ , angulus bgd minimus est, dum ad verticem, hoc est ad extremum axis ag consistit. // Igitur et anguli lht bte (quippe qui semper quantitatem anguli bgd propter aequidistantiam linearum, concomitantium) minimi sunt, dum zh⁴⁶⁹ ipsis ab gd axium extrema connectentibus aequidistat. // Et ideo tunc zh maxime oblique incidit ipsis bg kl ordinate ductis.//

[S:84] // Vel sic, quoniam, per 9^um lemmatum , angulus abg maximus est, dum apud verticem, id est ad extremum db axis consistit; propterea ipsi anguli thk etg singuli iam⁴⁷⁰ semper aequales angulo abg maximi sunt, dum zh diameter ipsis ab gd axium extrema connectentibus aequidistat.

// Quod demonstrandum proponitur.

[A:64r]

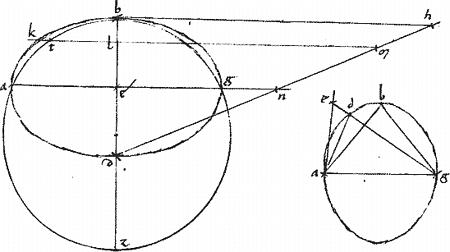
Manifestum est igitur, quod in ellipsi, diameter oblique incidens tangenti, ceterisque sibi ordinatis, incidet ad duos angulos, acutum et obtusum: qui singuli sunt aequales angulis parallelogrammi intra sectionem descripti, cuius duo latera opposita sunt ex numero ordinatarum.

SCHOLIUM

Et ideo diameter, maxime oblique incidens tangenti incidit ad duos angulos parallelogrammi habentis angulos maxime acutos, et maxime obtusos, et axes sectionis pro diametris⁴⁷¹.

Sic, lemmatis his praemissis, negotium circa angulos in ellipsi factos optime discussum est, et brevissime singula demonstrata. Quorum quidem vix particulam, et eam obscurissime tetigerat Apollonius.

Quibus fundamentis iactis, ultimum secundi libelli Conicorum problema non minus facile, quam breviter effectum dabimus.