52a Data ellipsi, tangentem ducere, quae ad ductam per tactum diametrum angulum faciat aequalem dato acuto. // Oportet utique datum acutum non minorem esse angulo, ad quem maxime obliqua diameter incidit apud tactum ipsi tangenti, ceterisque sibi ordinatis.
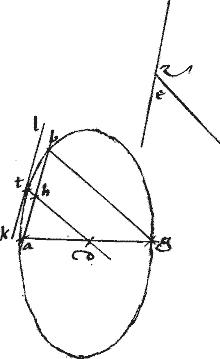
Sit data ellipsis abg // cuius minor axis ag // centrum d // datus acutus angulus e.
// Oportet ducere tangentem, quae cum ducta per tactum diametro angulum faciat angulo e aequalem. // Oportet autem angulum e non minorem esse angulo, ad quem maxime obliqua diameter incidit tangenti in data ellipsi. // Secus enim problema non esset472 possibile.
// Sed talis angulus, ad quem maxime obliqua diameter incidit tangenti, per praecedentem, aequalis est angulo verticali super minorem axium in ellipsi posito. // Igitur angulus e non minor erit tali angulo verticali.
// Itaque, per 10um lemmatum , constituatur supra minorem axim ag ad periferiam, ipsi angulo e dato aequalis angulo abg. // Sectaque ab per aequalia apud h coniungatur dh et producatur ad periferiam ad t punctum.
// Et per 49am huius, tangens sectionem apud t ducatur ktl. // Quae per 6am huius, aequidistans erit ipsi ab. // Et ideo angulus ktd aequalis erit angulo ahd.
// Sed angulus ahd aequalis angulo abg (quoniam per 2am 6i Euclidis ipsae hd bg aequidistantes) angulus autem abg angulo dato e fuit aequalis. // Ergo et angulus e datus aequalis est angulo ktd
// Itaque ducta est tangens ktl faciens cum td diameter angulum ktd aequalem angulo dato e. // Quod erat faciendum.
// Vel sic capiatur angulus obtusus z qui cum angulo dato e confiat duos rectos. // Et [A:64v]
quoniam angulus minimus super473 minorem axim ellipsis, cum angulo maximo supra maiorem axim (ad quos videlicet per praemissam diameter maxime oblique incidit tangenti) conficit duos rectos: quandoquidem tales anguli sunt acutus et obtusus eiusdem parallelogrammi: ideo cum datus angulus e non minor sit angulo supra minorem axim : iam et angulus z non maior erit angulo supra maiorem axim474 ad verticem posito. // Itaque, per 11um lemma, constituatur super axim ag qui maior nunc supponatur , ad periferiam ipsi angulo z aequalis angulus abg.
// Et caetera fiant, ut prius: donec angulus k475 td quem facit ktl tangens cum td diametro per tactum ducta arguatur aequalis angulo z et perinde angulus l476 td angulo e dato aequalis. // Quod quidem faciendum proponitur.