50^a Data coni sectione, tangentem ducere, quae ad axim, sive ad diametrum ductam³⁷¹ aequalem angulum contineat dato acuto.

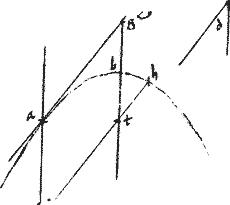
Sit coni sectio, primum parabole ab. // Cuius axis, sive diameter bg. // Datusque angulus d acutus.

// Oportet utique ducere lineam, quae tangat sectionem, faciatque ad axim sive diametrum bg angulum, angulo d aequalem³⁷².

//³⁷³ Producatur axis, sive diameter: ponaturque bth angulus aequalis angulo d. // Coincidet utique th utrinque producta sectioni: coincidat per 27^am praemissi, apud h z. // Seceturque hz bifariam apud e. // Ipsique gb parallelus agatur ea secans periferiam apud a. // Eritque per 46. praemissi ae diameter: et ipsa zh ordinate ducta ad talem diametrum. // Itaque ipsi zh parallelus agatur ag. // Quae per 17^am praemissi, tanget sectionem apud a. // Eritque angulus agb aequalis angulo bth coalterno et perinde angulo d. // Ergo factum, quod faciendum proponebatur.

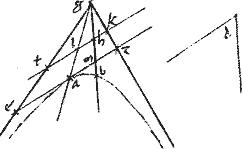
Sit deinde hyperbole ab. // Cuius axis sive diameter bg. // Centrumque g. // Datusque angulus d et reliqua.

// Sint non tangentes³⁷⁴ sectionis egz. // Ponaturque angulus bht aequalis angulo d qui utique [S:77] sit³⁷⁵ maior angulo egb ut ipsa th concurrat non tangentibus egz apud puncta t k³⁷⁶. // Et³⁷⁷ secetur bifariam tk³⁷⁸ apud l. // Et producatur gl donec secet periferiam apud a.

// Et per a ducatur ipsi tk aequidistans eaz. // Quare, propter similitudinem sicut ipsae tl lk aequales³⁷⁹ invicem³⁸⁰. Ita et ea³⁸¹ az inter se³⁸² aequales: et perinde³⁸³ ea tanget sectionem apud a per 9^am huius. // Secet autem ez ipsam gb apud m eritque³⁸⁴ angulus amb aequalis angulo bht sibi intrinsecus posito³⁸⁵.

// Rursum ergo factum, quod faciendum proponitur.

[A:58v]

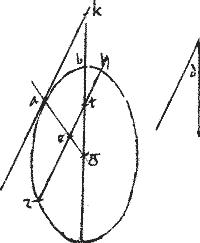
Sit demum ellipsis ab ab³⁸⁶ // Cuius axis vel diameter gb. // Centrum g. // Datus angulus d et reliqua.

// Ponatur ipsi d angulo aequalis angulus ztg. // Et producatur zt utrinque ad periferiam ad puncta z h. // Et secetur bifariam apud e. // Et coniuncta³⁸⁷ ge producatur ad periferiam ad punctum a. // Eritque, per 47. [[ag]]³⁸⁸ diameter: et ipsa zh ordinate ducta. // Agatur ergo ipsi zh parallelus ak occurrens apud k diametro gb productae. // Quae per 17^am praemissi, tanget sectionem apud a. // Eritque, propter aequidistantiam linearum, angulus akg ipsi angulo³⁸⁹ etg et perinde ipsi d dato aequalis: quod faciendum proponitur.

SCHOLIUM

Notandum, quod in parabola, si ag ponatur tangens sectionem, aequidistabit ipsi zh bifariam sectae, per 5^am huius. // Quare, et per conversionem eiusdem 5^ae cum ag ponatur ipsi zh bifariam divisae, parallelus in problemate, erit utique tangens sectionem apud a punctum.

// Similiter et in ellipsi, si ak ponatur tangens periferiam, aequidistabit ipsi zh bifariam sectae per 6^am huius. // Quare et per conversionem eiusdem 6^ae cum ak ponatur in problemate ipsi zh bifariam divisae parallelus, erit utique tangens ellipsim apud a punctum. Sicut faciendum proponitur.

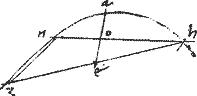
Verum quod zh bifariam divisa in puncto e per diametrum ae ordinate ducta sit ad ipsam ae diametrum, patet sic. // Nam si zh ordinate ducta non sit; ordinate ducatur hn secta per diametrum apud o. // Aequalis ergo est ho ipsi on. // Et connexa zn aequidistabit ipsi ae per 2^am 6ⁱ Euclidis. // Quod per 22^am et 23^am praemissi impossibile est: concurrit enim ei. // Itaque per punctum h non alia quam zh ordinate ducitur ad ae diametrum.