49a Coni sectione data, et puncto non intra sectionem; ducere a puncto lineam ad unum314 tangentem sectionem.
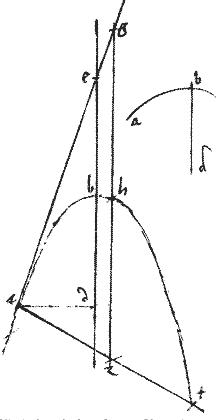
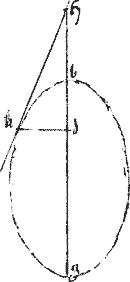
Sit data coni sectio prius parabole ab cuius axis bd. // Oportet utique a dato puncto, quod non est intra sectionem, ducere tangentem lineam. // Datum autem315 punctum, vel in sectione316, vel in axi, vel in aliquo extra loco.
// Sit igitur primum in periferia, et sit a. // Et fiat tangens et317 sit ae et318 kathetus ducatur ad datus iam positione: ipsique db aequalis be per 35am praemissi319, datum itaque e.
// Componitur autem sic, ducatur ab a kathetus ad et ponatur ipsi bd aequalis be et coniungatur ae. Manifestum utique quod ae tangit sectionem apud a per 33am praecedentis.
Sit rursus datum punctum e in axi fiat et ducatur tangens ae et kathetus ad igitur320 per 35am praecedentis be aequalis bd itaque ed datur positione et magnitudine: datur ergo d cumque detur da dabitur a datum fuit e datur ergo ae positione.
// Componetur autem sic: ponatur bd aequalis be et a puncto d excitetur ad rectos da et coniungatur ae quae per 33am praemissi apud a tanget sectionem.
Quod si datum punctum sit b summitas scilicet axis. Tunc ab ipso b puncto ad rectos axi, excitata tanget sectionem, per 32am praemissi.
Demum sit datum punctum extra axim, ut g fiat et sit tangens ga et per g ducatur gz aequidistans axi bd positione igitur datur gz et a puncto a ordinate ducatur ad gz diametrum linea az eritque per 35am praemissi, gh aequalis hz ipsam321 autem az aequidistans iam per 5am huius, tangenti apud h positione datur: cum z datum sit. Itaque et a punctum datum. // Componetur autem sic. Ducatur per g ipsi bd aequidistans gz ipsique gh aequalis ponatur hz et ducatur za penes tangentem apud h et coniungatur ag namque, per 46am praemissi, az ordinate applicatur: et per 33am eiusdem ag tanget apud a sectionem: quod faciendum proponitur.
[S:75] Data hyperbola, a dato puncto extra, eam tangentem ducere.
Sit hyperbole, cuius axis gbd. // Centrum t. // Non tangentes322 et tz.
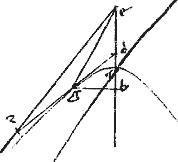
// Datum autem punctum, aut erit in sectione, vel in axi, vel in altera non tangentium323, vel denique in aliquo324 inter non tangentes325 ac sectionem.
// Si quidem omnis linea vel ab angulo non tangentium326 hoc est a centro, vel ab aliquo puncto diametri supra centrum ducta in sectione secat sectionem per 29am praemissi, atque per 2am huius. // Quare non speres inde tangentem ducere.
// Sit itaque primo datum punctum327 in sectione, ut a et fiat: et sit328 tangens ah et ducatur kathetus ad transversa vero diameter sit329 bg. // Erit utique per 36am praemissi, sicut gd ![]() db sic gh
db sic gh ![]() hb. // Ratio autem gd
hb. // Ratio autem gd ![]() db data. Ergo et ratio gh
db data. Ergo et ratio gh ![]() hb datur. // Sed gb data.// Datum330 ergo punctum h datum autem fuit punctum a. // Igitur ah positione331. // Componetur sic. Ducatur a puncto a kathetus ad. // Et sicut gd
hb datur. // Sed gb data.// Datum330 ergo punctum h datum autem fuit punctum a. // Igitur ah positione331. // Componetur sic. Ducatur a puncto a kathetus ad. // Et sicut gd ![]() db sic fiat gh
db sic fiat gh ![]() hb et coniungatur ah quae per 34am praecedentis, tanget apud a sectionem.
hb et coniungatur ah quae per 34am praecedentis, tanget apud a sectionem.
Rursus utique sit datum punctum in axi, quod sit h et fiat, et ducatur ah tangens, et kathetus ducatur ad. // Per eadem utique erit ut gh ![]() hb sic gd
hb sic gd ![]() db. // Et est data gbd datum igitur d sed ad rectos da datur ergo da positione: ipsiusque332 a punctum in periferia. Datum autem et h. // Igitur ah positione333. // Componetur autem sic fiat ut gh
db. // Et est data gbd datum igitur d sed ad rectos da datur ergo da positione: ipsiusque332 a punctum in periferia. Datum autem et h. // Igitur ah positione333. // Componetur autem sic fiat ut gh ![]() hb sic gd
hb sic gd ![]() db. // Et ad rectos axi excitetur da et coniungatur ah quae ut prius, per 34am praemissi, apud a tanget sectionem.
db. // Et ad rectos axi excitetur da et coniungatur ah quae ut prius, per 34am praemissi, apud a tanget sectionem.
Eisdem subiectis. Sit datum punctum c intra angulum etz.
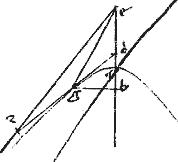
// Fiat et sit ca tangens. // Et coniuncta ct producatur rursum et ad periferiam: ponaturque ipsi tl aequalis nt334.
// Omnia igitur data. // Ducatur ordinate am ad ipsam mn diametrum. // Eritque, per 36am praemissi, sicut nm ![]() ml sic nc
ml sic nc ![]() cl. // Datur autem ratio nc
cl. // Datur autem ratio nc ![]() cl propter t c puncta data: datur ergo ratio335 nm
cl propter t c puncta data: datur ergo ratio335 nm ![]() ml. // Datum autem l igitur et m punctum datur. // Sed ma tangenti apud l aequidistans datur positione: datur ergo a punctum in periferia.
ml. // Datum autem l igitur et m punctum datur. // Sed ma tangenti apud l aequidistans datur positione: datur ergo a punctum in periferia.
// Datum etiam est c igitur ac tangens positione336.
// Componetur autem sic ct coniuncta producatur: et ponatur tn aequalis lt.
// Utque nc ![]() cl sic [[sit]]337 nm
cl sic [[sit]]337 nm ![]() ml et ducatur ma aequidistans tan- [A:56v] genti apud l.// Et coniungatur ca quae per 34am praemissi, apud a punctum tanget sectionem.
ml et ducatur ma aequidistans tan- [A:56v] genti apud l.// Et coniungatur ca quae per 34am praemissi, apud a punctum tanget sectionem.
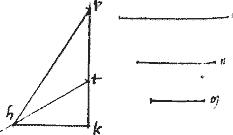
Eisdem subiectis. Sit datum punctum z in una non tangentium338. // Fiat, et sit zae tangens, quae, per 3am huius coincidit non tangentibus339 hinc, et inde. // Et ducatur ipsi et aequidistans ad. // Et, quoniam per 3am huius, za aequalis ae erit, per 2am sexti zd aequalis dt. // Datum igitur d et ipsa ad positione. // Quare a punctum in periferia datur. Sed et z datum. // Ergo et zae positione.
// Componetur autem sic. Secetur zt bifariam apud d ipsique te aequidistans ducatur da et producatur zae. // Et quoniam zd aequalis dt erit et za aequalis ae. // Quare per 9am huius zae apud a tangit340 sectionem.
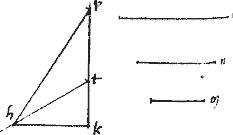
Eisdem subiectis, sit datum punctum sub angulo extrinseco non tangentium341, quod sit c. // Fiat utique, sitque ca tangens: et coniuncta ct dabitur positione. // Cui aequidistans per g utcumque relictum in sectione punctum, ducatur gd quae per medium secetur, apud e et coniuncta te producatur diameter iam positione existens coniugata ipsi tc et periferiam secans apud b. // Ponaturque ipsi bt aequalis th. // Et per a tactum342 ducatur al aequidistans ipsi bt. // Et quoniam bh cl coniugatae sunt diametri: tangens autem ac et ipsa al penes bh iam, per 38am praecedentis, ![]() ctl aequale est
ctl aequale est ![]() quod ex 2a semidiametro, hoc est quadrante speciei ad bh adiacentis. Datur autem species, datis iam pridem sectionis diametris: datur ergo
quod ex 2a semidiametro, hoc est quadrante speciei ad bh adiacentis. Datur autem species, datis iam pridem sectionis diametris: datur ergo ![]() ctl. // Sed ct data, datis iam punctis inclusa: datur igitur tl. // Estque positione datum t datum ergo l.
ctl. // Sed ct data, datis iam punctis inclusa: datur igitur tl. // Estque positione datum t datum ergo l.
// Igitur la aequidistans ipsi bh positione datae datur positione. // Quare a punctum datum: sed c datum est. Ergo et ca positione.
// Componetur autem sic.// Coniungatur ct et producatur, cui aequidistans, per g relictum punctum agatur in sectione gd quae bifariam secetur apud e.
[S:76] // Et coniungatur et secans periferiam apud b ipsique bt aequalis ponatur th. // Eruntque hb cl coniugatae diametri: quoniam343 cl ordinate ducta ad ipsam bh. // Ponatur utique ![]() ctl quadrans speciei ad [A:57r] bh adiacentis. // Et ducatur la aequidistans bh et coniungatur ca. // Quae per conversionem 38ae praecedentis libri apud a tanget sectionem.
ctl quadrans speciei ad [A:57r] bh adiacentis. // Et ducatur la aequidistans bh et coniungatur ca. // Quae per conversionem 38ae praecedentis libri apud a tanget sectionem.
// Productis autem rursum non tangentibus344 ad z p iam a quovis puncto dato intra ztp impossibile est duci tangentem. Nam a tali puncto linea deducta ad periferiam sectionis ab secat utramque non tangentium345 ad angulum extrinsecum, quare per 16am huius secabit sectionem. // Vel sic, si possibile346 talem lineam tangere sectionem: iam per 24am praemissi libri, coincidet diametro bh et ideo, per 29am eiusdem secabit sectionem: quod est contra suppositum.
Data ellipsi a dato347 dato non intra puncto, tangentem ducere.
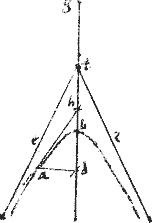
Sit ellipsis ab. // Cuius axis gd. // Datum punctum primo in periferia, quod sit a. // Fiat, et sit ah tangens. // Et ab a ad axim kathetus ducatur ad. // Eritque datum d. // Atque per 36am praecedentis, ut gd ![]() db sic gh
db sic gh ![]() hb.
hb.
// Datur autem ratio gd ![]() db. // Ergo et ratio gh
db. // Ergo et ratio gh ![]() hb datur, et disiunctim ratio gb
hb datur, et disiunctim ratio gb ![]() bh dabitur. // Itaque bh datur: et punctum h datum: sed a datum: igitur et ah positione.
bh dabitur. // Itaque bh datur: et punctum h datum: sed a datum: igitur et ah positione.
// Componetur autem sic. Ducatur kathetus ad. // Sitque sicut gd ![]() db sic gh
db sic gh ![]() hb. // Et coniungatur ah quae, per 34am praemissi, iam apud a tanget sectionem.
hb. // Et coniungatur ah quae, per 34am praemissi, iam apud a tanget sectionem.
Rursum sit datum punctum c extra sectionem. // Fiat et sit tangens ca. // Et per a348 et ipsum t centrum agatur diameter cltn periferiae coincidens ad puncta l n data iam positione. // Ducta quam349 am ordinate ad diametrum / erit, per 36am praemissi, sicut nc ![]() cl sic nm
cl sic nm ![]() ml.
ml.
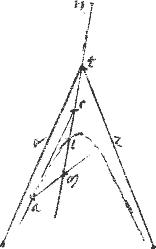
// Datur autem350 ratio nc ![]() cl351 datur ergo et ratio nm
cl351 datur ergo et ratio nm ![]() ml352 datum ergo m punctum. Sed ma aequidistat tangenti ad l per 6am huius: ergo datur positione: et ideo a datum353: et perinde ac positione. // Componetur autem sic. Ducta iam diametro cltn sit sicut nc
ml352 datum ergo m punctum. Sed ma aequidistat tangenti ad l per 6am huius: ergo datur positione: et ideo a datum353: et perinde ac positione. // Componetur autem sic. Ducta iam diametro cltn sit sicut nc ![]() cl sic nm
cl sic nm ![]() ml. // Et ducatur ordinate ma354 // Et coniungatur ac quae sicut prius, per 34am praecedentis apud a tanget sectionem.
ml. // Et ducatur ordinate ma354 // Et coniungatur ac quae sicut prius, per 34am praecedentis apud a tanget sectionem.
// Itaque absolutum problema: factumque, quod faciendum proponebatur.
Panhormi 23 feb. 1547355
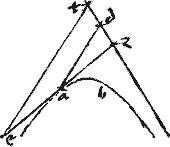
358 Data coni sectionem, tangentem ducere, quae ad axim angulum faciat ad eandem sectioni aequalem dato acuto.359
Sit coni sectio prius parabole, cuius axis ab.360
// Oportet utique ducere lineam, quae tangat sectionem faciens ad axim ab angulum ad eandem sectioni aequalem dato acuto.361
// Fiat tangens et sit dg. // Ordinate autem gb hoc est ad rectos axi. // Et coniungatur ag. // Et [[quoniam]] angulus b rectus; et qui ad d datus; ideo et qui ad g datus;362
// itaque ratio db ![]() bg data. Sed db bg positione; // igitur et dg positione.363
bg data. Sed db bg positione; // igitur et dg positione.363
// Componetur autem sic. // Sit datus angulus acutus ezh. // Et kathetus eh. // Et zh bifariam secetur apud t. // Et coniungatur te. // Et ponatur angulus bag aequalis angulo hte. // Et ducatur kathetus bg. // Et ipsi ba aequalis ponatur ad. // Et coniungatur gd. / Quae per 33am praecedentis libri tanget apud g sectionem. // Et quoniam anguli ad hb recti: et anguli eth gab aequales: ideo similia sunt ![]()
![]() the abg. // Quare per 4am 6i Euclidis sicut th
the abg. // Quare per 4am 6i Euclidis sicut th![]() he sic ab
he sic ab![]() bg. // Sed sicut zh
bg. // Sed sicut zh ![]() ht sic db
ht sic db ![]() ba. // Ex aequo igitur, sicut zh
ba. // Ex aequo igitur, sicut zh ![]() he sic db
he sic db ![]() bg. // Cumque anguli hb sint aequales: // iam per 6am Sexti Euclidis aequianguli sunt
bg. // Cumque anguli hb sint aequales: // iam per 6am Sexti Euclidis aequianguli sunt ![]()
![]() zhe dbg. // Ergo anguli, qui apud zd aequales. // Itaque tangens ducta est dg faciens cum axe db angulum d aequalem dato angulo z. // Quod faciendum proponitur.364
zhe dbg. // Ergo anguli, qui apud zd aequales. // Itaque tangens ducta est dg faciens cum axe db angulum d aequalem dato angulo z. // Quod faciendum proponitur.364
365 Sit sectio hyperbole. Et fiat, et sit tangens gd. // Centrum autem sectionis e. // Et coniungatur ge. // Et kathetus gb.366
// Ratio igitur ipsius ![]() ebd
ebd ![]()
![]() bg data: est enim per 21am praemissi, quae transversae ad rectam. // Angulus autem gde datus: et qui ad b rectus. // Datur ergo
bg data: est enim per 21am praemissi, quae transversae ad rectam. // Angulus autem gde datus: et qui ad b rectus. // Datur ergo ![]() gde specie. // Et perinde ratio db
gde specie. // Et perinde ratio db![]() bg datur. // Quae si auferatur a ratione
bg datur. // Quae si auferatur a ratione ![]() ebd
ebd ![]()
![]() bg superest ratio eb
bg superest ratio eb![]() bg data. // Sed eb bg positione dantur: ergo et eg positione.367
bg data. // Sed eb bg positione dantur: ergo et eg positione.367
// Ducatur non tangens ez cui, per 3am huius, coincidet dg tangens: // coincidat ad z. // Maior igitur erit angulus zdb angulo zed extrinsecus videlicet intrinseco. // Oportebit itaque in compositione datum angulum maiorem esse dimidio anguli contenti sub non tangentibus.
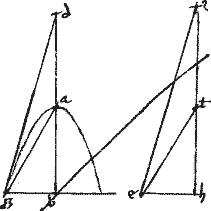
// Itemque si ponatur gdb datus angulus: et ablata ratione db![]() bg ad ipsa ratione tranversae ad rectam, supererit iam ratio eb
bg ad ipsa ratione tranversae ad rectam, supererit iam ratio eb![]() bg ita ut maior sit eb quam bd.368
bg ita ut maior sit eb quam bd.368
// Componetur itaque problema sic. // Sit datus acutus htk data hyperbolae quam prius. // Ducatur kathetus hk. // Sitque l tranversa sectio[A:58r]nis. Recta vero m. // Deinde sicut tk![]() kh sic fiat l
kh sic fiat l![]() n. // Tum autem sicut n
n. // Tum autem sicut n![]() m sic fiat pk
m sic fiat pk![]() kh maior autem erit pk quam kt sic maior erat eb quam bd. // Et connectatur hp. // Eritque angulus kph minor angulo bez dimidio scilicet anguli sub non tangentibus contenti, sicut patuit. // Ponatur itaque ipsi p angulo aequalis beg angulus. // Ductoque katheto gb sit sicut kt
kh maior autem erit pk quam kt sic maior erat eb quam bd. // Et connectatur hp. // Eritque angulus kph minor angulo bez dimidio scilicet anguli sub non tangentibus contenti, sicut patuit. // Ponatur itaque ipsi p angulo aequalis beg angulus. // Ductoque katheto gb sit sicut kt![]() tp sic et bd
tp sic et bd![]() de. // Et coniungatur dg.369
de. // Et coniungatur dg.369
// hucusque Castellobono370