[S:55] 4a Duabus datis lineis angulum continentibus, et puncto intra angulum, describere per punctum coni sectionem vocatam hyperbolen; cuius non tangentes sint ipsae datae lineae.
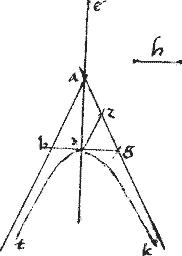
Sint duae lineae ba ag contingentem angulum bag continentes: et datum sit quoddam58 punctum, quod sit d.
// Oportet hyperbolen describere, quae per d punctum eat. Et cuius non tangentes sint ba ag.
// Coniungatur ad et producatur ad e59 sitque ipsi da aequalis ae. // Et per d ducatur dz aequidistans ipsi ab. // Et ponatur ipsi az aequalis zg. // Et coniuncta gd producatur ad b. // Et fiat ![]() deh aequale
deh aequale ![]() bg. // Et producta ad describatur circa ipsam hyperbole, per 53am praecedentis libri, cuius transversa diametros sit ed recta vero h ut ordinate ductae possint adiacentia60 ad ipsam h sub61 latitudine sub ipsis ad summitatem receptis, et excedentia specie simili ei, quod sub deh rectangulo. Quae hyperbole sit tdk transiens iam per datum punctum d. // Cumque dz sit ipsi ab parallelus; et gz za aequales; erunt, per 2am sexti Euclidis et bd dg aequales. // Quare
bg. // Et producta ad describatur circa ipsam hyperbole, per 53am praecedentis libri, cuius transversa diametros sit ed recta vero h ut ordinate ductae possint adiacentia60 ad ipsam h sub61 latitudine sub ipsis ad summitatem receptis, et excedentia specie simili ei, quod sub deh rectangulo. Quae hyperbole sit tdk transiens iam per datum punctum d. // Cumque dz sit ipsi ab parallelus; et gz za aequales; erunt, per 2am sexti Euclidis et bd dg aequales. // Quare ![]() bg quadruplum erit ad
bg quadruplum erit ad ![]() gd. // Et ideo
gd. // Et ideo ![]() gd quadrans speciei sectionis, quae scilicet sub de h diametris62 continetur. // Igitur per primam huius, ipsae ba ag sunt non tangentes63, ipsius tdk descriptae hyperboles. Et perinde factum est, quod faciendum proponebatur. [A:41v]
gd quadrans speciei sectionis, quae scilicet sub de h diametris62 continetur. // Igitur per primam huius, ipsae ba ag sunt non tangentes63, ipsius tdk descriptae hyperboles. Et perinde factum est, quod faciendum proponebatur. [A:41v]