3^a Si hyperbolen linea tangat, coincidet utrique non tangentium⁴⁴, et per aequalia secabitur apud tactum: et quadratum ex utravis portionum ipsius, aequale erit quadranti speciei⁴⁵ factae ad ductam diametrum per tactum.

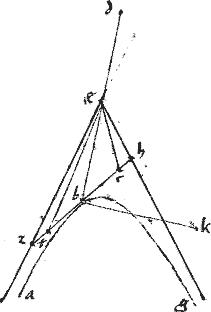
Sit hyperbole abg. // Centrum e. // Non tangentes ze eh. // Et tangat ipsam tbc⁴⁶ ad punctum b.

// Dico quod tc tangens producta coincidet ipsis ze eh.

// Si enim possibile est, non coincidat. // Et coniuncta eb producatur ed aequalis ipsis eb⁴⁷ // Eritque per 47^amprimi Conicorum bd diameter cuius recta sit bk. // Et ponatur quartae parti speciei, quae sub db⁴⁸ bk aequale tam ipsius bt quam ipsius bc. Et coniungantur et ec. // Eruntque, per primam huius, et ec non tangentes⁴⁹, quod per praecedentem est impossibile. // Igitur tc producta coincidet ipsis ze eh quod est primum ex demonstrandis. Coincidat ad zh.

// Dico item quod zb sicut et bh est quarta pars speciei, quae sub db bk.

// Non enim, sed si possibile est, sit quartae parti speciei aequale bt nec non bc. Eruntque, per primam huius, ipsae te ec non tangentes⁵⁰: suntque per hypothesim non tangentes ze eh quod, per praecedentem est impossibile.

// Igitur zb sicut et bh aequale erit quartae parti speciei, quae sub db bk. // Quod supererat demonstrandum. Ergo et ipsae zb bh tangentis inter tactum et non tangentes, inclusae portiones aequales sunt, quemadmodum proponebatur ostendendum.

Per quodvis relictum⁵¹ in hyperbola punctum penes alteram non tangentium⁵² acta linea non alibi, quam in ipso puncto coincidit sectioni: ac sub eo semper intra sectonem fertur.

Sit hyperbole bh cuius centrum g. non tangentes⁵³ dge. Relictum utcumque punctum b.

// Dico quod linea per b utpote bk ipsarum dg ge alteri, ut ipsi gd aequidistans in ipso solum b puncto coincidit sectioni / et sub eo deducta semper intra sectionem fertur.

// Sit enim dbe sectionem tangens apud b. // Coniungatur et⁵⁴ gb [A:41r] eique ponatur aequalis ga.

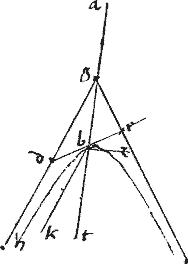
Eritque agb diameter per 47^am primi, Conicorum: atque⁵⁵ per praemissam ipsae db be aequales: et earum utraque potens quadrantem speciei sub ab diametro, et bz recta⁵⁶ contentae. Quare per additam post primam huius, linea bk ab ipsa b summitate ipsi gd non tangenti⁵⁷ aequidistans, non alibi, quam in ipso b summitatis puncto sectioni coincidet, et sub eo continuata semper intra sectionem feretur. // Quod erat demonstrandum.