38a Si contrapositas duae lineae tangant coincidentes; quae a concursu coniungitur ad mediam268 tactus coniungentes269, diameter erit contrapositarum coniugata ei tranversae, quae per centrum ducitur penes tactus coniungentem.
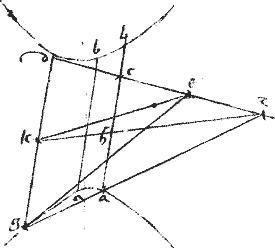
Sint contrapositae sectiones a b. // Tangentes autem ge ed. // Coniungens tactus gd. // Quae secetur bifariam apud k. // Et coniungatur ek. // Ipsi quoque gd aequidistans et per centrum ducta ab. // Coincidunt autem de ge per 31am huius.
// Dico iam quod ke diameter est coniugata ipsi ab transversae.
// Secus enim sit diameter ipsi ab coniugata, ipsa kz quae iam coincidet ipsi de quandoquidem tangens apud b ipsi kz ordinate applicatae aequidistans. Coincidit eidem de per 25am huius. // Coincidat itaque kz ipsi de apud z270 et coniungatur gz quae secabit sectionem, cum eg tangat. // Secet ergo gz sectionem apud a. // Et per a intelligatur inter sectiones ipsi gd aequidistans ab sive per centrum, sive aliam nil refert , concidens ipsi271 kz apud h ipsique de apud c. // Quoniam igitur diameter est kz coniugata transversae ipsius gd parallelo: iam per 16am praecedentis, ipsam [S:70] transversam, omnemque eius parallelum, sicut ipsam gd bifariam secat: igitur kz bifariam secabit ipsam ab unam ex parallelis. // Itaque ah aequalis hb.
// Verum quoniam gk aequalis272 kd ideo ah aequalis hc propter 
similitudinem. // Ergo ch aequalis hb. // Quod est impossibile. // Non ergo kz neque ulla alia praeter quam ke linea coniugata diameter erit ipsi transversae ipsius gd parallelo. // Quod fuit demonstrandum.
SCHOLIUM
Non autem te conturbet, quod primum ab lineam273 per sectionum centrum supposuimus ductam, ac deinde per punctum in quo gz secat periferiam sectionis. Posses enim utramque per se ducere, si lubet. Quamquam cum utraque aequidistet ipsi gd potest una et eadem esse, si extrema casu coincidant.
Manifestum est ergo, quod si lineae274, quae contrapositas tangunt, coincidant: tunc eius, quae tactus iungenti aequidistat, portiones tangentibus et periferiis sectionum inclusae sunt aequales.