37^a Si contrapositas linea secet non per centrum; quae a bifaria sectione ipsius ad centrum coniungitur, diameter est contrapositarum: coniugata ei transversae ²⁶⁴, quae a centro ducta aequidistat bifariam sectae.

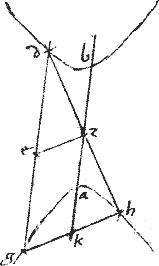
Sint contrapositae sectiones a b. // Quas secet linea gd non per centrum existens. // A cuius bifaria divisione e agatur ad centrum z linea ez. // Et ducatur ab aequidistans ipsi gd.

// Dico iam quod ab ez coniugatae sunt diametri sectionum.

// Coniungatur enim dz et producatur ad h in aliam sectionem, per 31^am praemissi. // Item connectatur gh cui²⁶⁵ ab producta coincidat apud k. // Eritque per 30^am praemissi dz aequalis ipsi zh cumque de sit aequalis ipsi eg iam per 2^am Sexti Euclidis aequidistans erit gh ipsi ez. // Unde ez gk kh invicem aequales²⁶⁶.

// Quare, per 5^am huius, tangens sectionem apud a aequidistabit ipsi [A:52r] gh quare et ipsi ez item et ipsi apud b tangenti per 31^am, huius.

// Itaque, per 48^am praecedentis ab secabit singulas harum aequidistantes in sectionibus bifariam: et perinde sectae ordinate ductae sunt ad ab diametrum. // Igitur ez ordinate ducta est ab ipso centro z.

// Igitur²⁶⁷, per 16^am praemissi ez coniugata diametros est ipsi ab transversae diametro.

// Quod fuit demonstrandum.