30a Si coni sectionem, vel circuli periferiam duae lineae tangentes coincidant: quae a concursu ducitur, diameter bifariam233 secabit lineam tactus coniungentem.
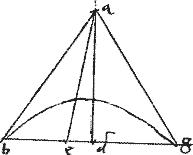
Sit coni sectio, vel circulus bg. // Tangentes ba ag coincidentes ad a. // Et coniungatur bg234. // Et ducatur per a diameter sectionis ad235
// Dico iam quod bd aequalis est ipsi dg.
// Non enim: sed si possibile est, sit be aequalis eg. // Et coniungatur ae. Eritque per praecedentem ae diameter sectionis236.
// Itaque si sectio ellipsis est, circulusve: erit a centrum sectionis extra ambitum: quod est impossibile.
// Si parabole, coincidunt diametri, quod est impossibile, aequidistat237 enim, per 46am praemissi.
// Si hyperbole, cum per 25am huius, a concursu sit intra angulum non tangentium238, erit iam a centrum intra angulum, sed per primam huius, centrum centrum239 hyperboles, est in ipso angulo non tangentium240: quod est impossibile.
// Non igitur bg alibi, quam in d puncto, per aequalia secatur.
// Quod fuit demonstrandum.
[S:67] Vel241 sic, diameter per punctum e ducta, in ellipsi aut circulo concurret cum ad diametro intra periferiam: in hyperbola vero concurret extra punctum a per 3am huius: in parabola demum aequidistabit ipsi ad per 46am praecedentis libri. Igitur a puncto e bifariae sectionis ipsius bg contactum puncta connectentis educta diameter, non incidit per a concursum tangentium: quod per praecedentem est impossibile. [[Adstruitur]]242 ergo propositum.
Si coni sectionem vel circuli periferiam duae linae tangentes coincidant: concursus fiet super ea diametro, ad quam ordinate applicatur quae tactus coniungit243.
Notandum quod haec propositio addita244 est eadem245 pene cum 29a246 praemissa: quamquam sub diversis terminis. Vel potest dici quod est corollarium, quodam ipsi 29ae247 ex qua pullulat, applicandum.