29^a Si coni sectionem, vel circuli periferiam duae lineae tangentes coincidant; quae a concursu ipsarum ad bifariam divisionem coniungentis tactus ducitur, linea, diameter est sectionis.

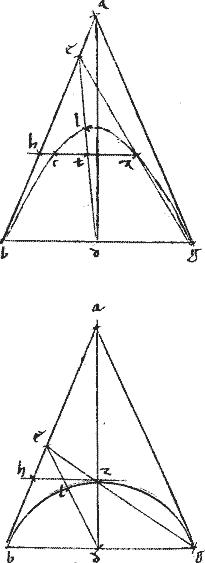
Sit coni sectio, vel circulus blg. // Tangentes ba ag coincidentes ad a. // Et coniuncta bg per aequalia secetur ad d. // Et coniungatur ad.

// Dico iam quod ad diameter est sectionis.

// Si enim possibile est, sit diameter dle²²⁷ et tunc eg coniuncta secabit utique sectionem: secet ad z. // Et per z ducatur ipsi bg aequidistans zh. // Quae aut secabit sectionem, aut tanget. // Secet primum, ut in punctis zc secet et ipsam de apud t.

// Et quoniam bd aequalis dg ideo et ht aequalis tz propter similitudinem . // Sed, quae apud l tangit sectionem, per 5^am vel 6^am huius, aequidistat ipsi bg. // Quandoquidem per 27^am praemissam bg non it per centrum, si sectio ellipsis vel circulus est. // Igitur et tangens apud l aequidistabit ipsi zh. // Quare, per 46^am vel 47^am praecedentis libri, ct aequalis²²⁸ ipsi tz. // Fuit autem zt aequalis th. // Ergo ht tc aequalis²²⁹, quod est absurdum.

// Nunc autem zh tangat sectionem apud z. // Itaque, per 5^am vel 6^am huius, aequidistabit ipsi²³⁰ ipsi bg tangens sectionem apud l et perinde aequidistabit ipsi hz cui coincidit: quod est absurdum.

// Vel sic, ducatur per l ipsi bg aequidistans et perinde ordinate applicata, quae, per 17^am cadet extra sectionem, quandoquidem per extremum diametri ducitur. Sed cadit intra, quoniam hz ipsi aequidistans tangit.

// Quod est absurdum. [A:50r] // Non est²³¹ ergo alia, quam ad sectionis²³² blg diameter. // Quod est demonstrandum.