23a Si in197 ad coniunctionem contrapositis198 ex centro quaedam ducatur ad quandam sectionum: et huic aequidistans ducatur coincidens tribus deinceps sectionibus; contentum sub portionibus ductae factis inter tres sectiones, duplum erit quadrati ab ea, quae ex centro, facti.
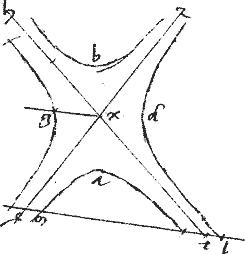
Sint ad coniunctionem cntrapositae sectiones a b g d. // Quarum centrum x. // Ipsaque xg ex centro ad sectionem g. // Ipsique xg aequidistans cl secans tres deinceps sectiones hoc est ipsas g d apud c l ipsamque a apud m.
// Dico iam quod ![]() cml aequale199 duplum est
cml aequale199 duplum est ![]()
![]() gx.
gx.
// Ducantur enim non tangentes200 sectionum exz hxt incidentes ipsi cl apud e t.
// Nam per primam secundi Euclidis201 ![]() emt
emt ![]() em tl simul aequalia sunt
em tl simul aequalia sunt ![]() eml itemque per eandem
eml itemque per eandem ![]() mlt vel lm ce (nam per 16am huius lt ce aequales)
mlt vel lm ce (nam per 16am huius lt ce aequales) ![]() em tl simul aequalia sunt
em tl simul aequalia sunt ![]() elt.
elt.
// Verum, posito communi ![]() lm ce
lm ce ![]() emt cum
emt cum ![]() em tl hoc est ipsum
em tl hoc est ipsum ![]() eml atque
eml atque ![]() lm ce aequalia sunt
lm ce aequalia sunt ![]() em tl cum
em tl cum ![]() lm ce hoc est ipsi
lm ce hoc est ipsi ![]() elt cum
elt cum ![]() emt
emt
|
|
// Ergo et ![]() tce
tce ![]() emt simul aequalia sunt
emt simul aequalia sunt ![]() lmc.
lmc.
// Est autem per 10am huius ![]() emt aequale
emt aequale ![]() to gx et per 11am huius
to gx et per 11am huius ![]() tce aequale eidem
tce aequale eidem ![]() gx. // Itaque
gx. // Itaque ![]() cml duplum
cml duplum ![]() gx. // Quod est demonstrandum.
gx. // Quod est demonstrandum.