22^a Si ad coniunctionem contrapositis ex centro linea ducatur ad quandam sectionum: etiam huic aequidistans, agatur coincidens uni deinceps sectionum et non tangentibus¹⁹¹: contentum sub portionibus actae factis inter sectionem et non tangentes¹⁹² aequale est quadrato eius, quae ex centro.

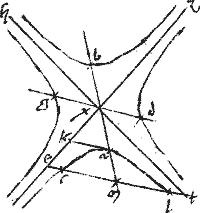
Sint ad coniunctionem contrapositae sectiones a b g d. // Non tangentes earum exz hxt.

// Et ex centro x ducatur quaedam linea ged¹⁹³ ad sectiones. // Eique aequidistans ducatur eclt in ipsis punctis secans sectionem et non tangentes¹⁹⁴.

// Dico iam quod ect aequale est gx.

// Sece[A:48r]tur enim bifariam cl apud m et coniuncta mx producatur secans sectiones a b apud a b.

// Eritque axb diameter sectionum a b quoniam per 5^am huius, tangens ad a aequidistat ipsi cl quare et¹⁹⁵ ad ipsam axb ordinate applicata est et ad eandem ordinate applicatur ipsa gxd.

// Igitur per 16^am praemissi, ab gd coniugatae diametri sunt.

// Ideoque, ex ultima praecedentis libri, gx poterit quadrantem speciei ad ab adiacentis.

// Verum, per 10^am huius, ect est quadrans eiusdem speciei.

// Ergo et ipsum ect aequale erit ipsi gx.

// Quod fuit de[S:64]monstrandum.

Manifestum est ergo quod et ipsius ka tangentis sectionem a est, quod ex gx¹⁹⁶.