21a Iisdem subiectis, demonstrandum quod concursus tangentium181 sit apud unam non tangentium182.
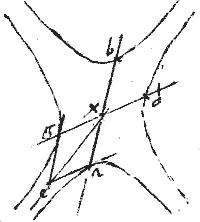
Sint ad coniuntionem contrapositae sectiones: quarum diametri ab gd. // Centrum x183 // Et tangentes ducantur ae ge.
// Dico iam quod punctum e est in una non tangentium184.
// Nam cum ab gd sint iam185 coniugatae diametri: et ideo, per 16am praecedentis, utraque sit ordinate ducta respectu alterius. Erit gx ordinate ducta ad ab item ea tangens ordinate ducta ad eandem per [[additam]]186 32ae praemissi, vel per 47am eiusdem, vel per corollarium 51ae eiusdem.
// Quare gx ea aequidistantes sunt.
// Et similiter ostendam, quod ax eg sunt aequidistantes.
// Parallelogrammum igitur aegx187 et ideo per 34am primi Euclidis ae gx aequales, itemque ge ax aequales.
// Sed per ultimam praemissi gd potest speciem adiacentem ipsi ab et ideo gx potest quadrantem eiusdem speciei.
// Igitur et ae potest eumdem quadrantem.
// Similiter ostendam, quod ge potest quadrantem speciei adiacentis ad gd.
// Quare, per primam huius, xe coniuncta non tangens188 erit tam ipsius a quam ipsius g specierum189. // Punctum ergo e concursus tangentium, est in ipsa xe non tangente190.
// Quod fuit demonstrandum.