[A:46v] [S:62] 20a Si unam contrapositarum ad coniunctionem linea tangat: et per centrum ipsarum ducantur duae linae, quarum haec quidem per tactum: illa vero penes tangentem usque quo coincidat uni deinceps sectionum; tangens sectionem apud coincidentem linea aequidistans erit ductae per tactum et centrum. Et ipsae per centrum tactusque iam ductae, coniugatae diametri contapositarum erunt.
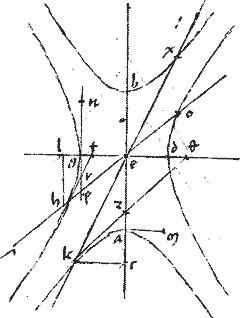
Sint ad coniunctionem contrapositae a b g d. // Quarum diametri ab gd. // Centrum e. // Linea kz ![]() tangens sectionem a in puncto k. // Ipsa kex ducta per centrum ac tantum k quae, per 29am praecedentis, secabit ipsas a b sectiones apud k x. // Ipsa vero oeh ducta per centrum penes ipsam kz
tangens sectionem a in puncto k. // Ipsa kex ducta per centrum ac tantum k quae, per 29am praecedentis, secabit ipsas a b sectiones apud k x. // Ipsa vero oeh ducta per centrum penes ipsam kz ![]() et secans ipsas sectiones g d per 2am huius, quandoquidem secat angulum non tangentium, quas per 3am huius, secat ipsa kz
et secans ipsas sectiones g d per 2am huius, quandoquidem secat angulum non tangentium, quas per 3am huius, secat ipsa kz ![]() tangens, ipsi iam oeh parallelus. // Item ht tangens sectionem g apud h ubi oeh coincidit sectioni.
tangens, ipsi iam oeh parallelus. // Item ht tangens sectionem g apud h ubi oeh coincidit sectioni.
// Tunc dico iam quod
th aequidistat ipsi kex. // Quodque ho hx sunt coniugatae diametri sectionum.
// Sint enim ordinate ductae kc hl grp. // Et rectae diametri162 ad quas163 possunt applicatae sint am gn.
// Et, quoniam per ultimam praemissi libri, ba ![]() am sicut164 ng
am sicut164 ng ![]() gd. // Ac per 37am eiusdem, sicut ba
gd. // Ac per 37am eiusdem, sicut ba ![]() am sic
am sic ![]() ecz
ecz ![]()
![]() ck itemque ng
ck itemque ng ![]() gd sicut
gd sicut ![]() hl
hl ![]()
![]() elt. // Ideo, sicut
elt. // Ideo, sicut ![]() hl
hl ![]()
![]() elt sic
elt sic ![]() ecz
ecz ![]()
![]() ck.
ck.
|
Itemque
|
// Igitur superest ratio ec ![]() ck aequalis rationi hl
ck aequalis rationi hl ![]() lt. // Cumque sint anguli eck hlt aequales propter165 aequidistantiam reciprocam ordinate ductarum ck lh unius ad diametrum alterius.
lt. // Cumque sint anguli eck hlt aequales propter165 aequidistantiam reciprocam ordinate ductarum ck lh unius ad diametrum alterius.
// Iam per 6am Sexti Euclidis ![]()
![]() eck hlt sunt invicem aequiangula: et ideo angulus kec aequalis angulo lht.
eck hlt sunt invicem aequiangula: et ideo angulus kec aequalis angulo lht.
// Sed totus angulus ceh aequalis toti angulo lhe coalterno. // Igitur reliquus166 keh aequalis reliquo angulo the.
// Quare per 27am primi Euclidis lineae ke [A:47r] ht sunt aequidistantes: quod est primum ex propositis.
// Deinde sit sicut
ph ![]() hr sic th
hr sic th ![]() s. // Eritque ex 50a praemissi, linea s dimidium eius, ad quam possunt ordinate ductae ad diametrum ho in ipsis sectionibus g d.
s. // Eritque ex 50a praemissi, linea s dimidium eius, ad quam possunt ordinate ductae ad diametrum ho in ipsis sectionibus g d.
// Et quoniam sectionum a b secunda diameter est gd ideo ex 38a praecedentis ![]()
![]() e kc167 kc aequale168
e kc167 kc aequale168 ![]() ge nam ipsi ce parallelus ducta per k abscindit ex ipsa eg aequale ipsi ck.
ge nam ipsi ce parallelus ducta per k abscindit ex ipsa eg aequale ipsi ck.
// Quare per 16am Sexti Euclidis ![]() e
e ![]() ge
ge ![]() ck sunt continuae proportionales.
ck sunt continuae proportionales.
// Et ideo, per 17am eiusdem. Sicut ![]() e
e ![]() ck sic
ck sic ![]()
![]() e
e ![]()
![]() eg.
eg.
// Sed propter ![]()
![]()
![]() ez kcz similitudinem sicut
ez kcz similitudinem sicut ![]() e
e ![]() ck sic
ck sic ![]() z
z ![]() zk et per primam Sexti, sic
zk et per primam Sexti, sic ![]()
![]() ez
ez ![]()
![]() ezk.
ezk.
// Igitur sicut ![]()
![]() ez
ez ![]()
![]() ezk sic
ezk sic ![]()
![]() e
e ![]()
![]() eg.
eg.
// Sed, per 18am 6i sicut ![]()
![]() e
e ![]()
![]() eg sic
eg sic ![]()
![]() ez
ez ![]()
![]() egp vel
egp vel ![]() hte per [[additam]]169 42ae praemissi.
hte per [[additam]]169 42ae praemissi.
// Ut ergo ![]()
![]() ez
ez ![]()
![]() ezk sic
ezk sic ![]()
![]() ez
ez ![]()
![]() hte.
hte.
// Quamobrem ![]()
![]() ezk hte sunt aequalia invicem.
ezk hte sunt aequalia invicem.
// Verum ipsi anguli the ekz aequales170, propter aequidistantiam linearum eos continentium. // Igitur, per 14am Sexti Euclidis reciproca sunt latera aequos angulos continentia hoc est ht ![]() ek sicut kz
ek sicut kz ![]() he.
he.
// Et ideo, per 15am eiusdem, ![]() the aequale
the aequale ![]() lo171 ekz.
lo171 ekz.
// Et, quoniam sicut s ![]() th sic rh
th sic rh ![]() hp ut autem rh
hp ut autem rh ![]() hp sic ek
hp sic ek ![]() kz propter aequidistantiam linearum.
kz propter aequidistantiam linearum.
Ideo sic s ![]() th sic ek
th sic ek ![]() kz.172
kz.172
// Sed per primam Sexti173 , sicut s ![]() th sic174
th sic174 ![]() s eh
s eh ![]()
![]() the itemque sicut ek
the itemque sicut ek ![]() kz sic
kz sic ![]() ek
ek ![]()
![]() ekz.
ekz.
// Igitur sicut ![]() ek
ek ![]()
![]() ekz sic
ekz sic ![]() s eh
s eh ![]()
![]() the.
the.
// Et permutatim, sicut ![]() ek
ek ![]()
![]() s eh sic
s eh sic ![]() ekz
ekz ![]()
![]() the.
the.
// Fuit autem aequale ![]() ekz
ekz ![]() lo the [S:63] ergo et
lo the [S:63] ergo et ![]() ek aequale
ek aequale ![]() 175 s eh .
175 s eh .
// Verum ![]() s eh176 est iam quadrans speciei, quae adiacet diametro ho nam he dimidium177 ipsius ho et ipsa s dimidium eius, ad quam possunt ductae. Itemque
s eh176 est iam quadrans speciei, quae adiacet diametro ho nam he dimidium177 ipsius ho et ipsa s dimidium eius, ad quam possunt ductae. Itemque ![]() ek quadrans
ek quadrans ![]() ti kx quandoquidem ek dimidium178 ipsius kx.
ti kx quandoquidem ek dimidium178 ipsius kx.
// Igitur ![]() kx aequale179 speciei, quae adiacet diametro ho.
kx aequale179 speciei, quae adiacet diametro ho.
// Et similiter ostendam quod vicissim ipsa ho potest speciem adiacentem diametro kx.
// Quare per conversionem ultimae primi conicorum ipsae kx ho sunt comiugatae diametri contrapositarum sectionum ad coniunctionem quae sunt a b g d.
// Praeterea, quoniam utraque harum diametrorum incidit per contactum tangentis penes alteram ductae180 sibique ordinatae: ideo utraque ordinatae ducta est ad alteram: quarum utraque secat parallelos alterius bifariam, per 16am praemissi, si pa[A:47v]ralleli sint extra contrapositas diametri secantis: si intra per 47am eiusdem.
// Rursus ergo per diffinitionem kx ho sunt coniugatae diametri.
// Id quod iam restabat demonstrandum.