14a non tangentes129 et hyperbole in infinitum protractae propius, propiusque sibi ipsis approximant130: et omni dato spatio ad minus perveniunt spatium.
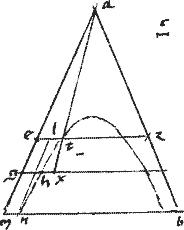
Sit hyperbole ht. // Nontangentes ba ag. // Datum spatium c.
// Dico iam, quod ab ag et sectio, magis magisque sibi continuatae131 adducuntur: et ad minus, quam c quantumvis exiguum spatium perveniunt.
// Ducantur enim penes tangentem lineae etz ghd et coniungatur at et producatur ad x.
// Et quoniam per 10am huius, ![]() ghd aequale est
ghd aequale est ![]() etz ideo per 15am Sexti Euclidis sicut dh
etz ideo per 15am Sexti Euclidis sicut dh ![]() tz sic et
tz sic et ![]() gh.
gh.
// Maior autem dh quam tz ergo et maior et quam gh.
// Similiter demonstrabimus quod spatia exteriora semper minora magis, magisque fiunt; donec relinquatur spatium ipso c minus.
// Capiatur enim ex ipsa et spatium el ipso c minus: et penes ipsam ag ducatur ln quae per praecedentem, coincidit sectioni.
// Coincidat apud n et agatur penes ez linea mnb. // Eritque per 34am primi Euclidis mn aequalis el et perinde minor spatio dato c. // Approximavit igitur ag non tangens132 sectioni ad minus, quam c spatium. // Verum itaque fuit quidquid proponebatur demonstrandum.