13am Si in114 segregato loco sub non115 tangentibus et sectione116 aequidistans ducatur quaedam linea alteri non tangentium, coincidet sectioni ad unum solum punctum.
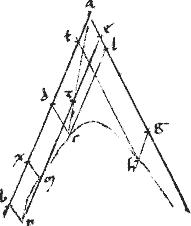
Sit hyperbole ch. // non tangentes117 ba ag. // Et per utcumque relictum punctum118 inter sectionem et non tangentes119 agatur ez penes ipsam ab.
// Dico iam quod
ez producta coincidet sectioni ad unum solum punctum.
// Si enim possibile est, non coincidat: et per contingens in sectione punctum h agantur hg ht non tangentibus120 paralleli: ponaturque ![]() lo ght aequale rectangulum aez et coniungatur az et producatur. Coincidet autem sectioni per 2am huius. Coincidat apud c et per c [S:59] agantur cd cl non tangentibus paralleli: compleaturque
lo ght aequale rectangulum aez et coniungatur az et producatur. Coincidet autem sectioni per 2am huius. Coincidat apud c et per c [S:59] agantur cd cl non tangentibus paralleli: compleaturque ![]() 121 dl.
121 dl.
// Eritque per praecedentem, ![]() 122 lcd aequale
122 lcd aequale ![]() ght. // Fuit autem
ght. // Fuit autem ![]() ght aequale
ght aequale ![]() aez. // Igitur
aez. // Igitur ![]() 123 aez aequale
123 aez aequale ![]() lcd pars scilicet toti. Quod est impossibile. // Coincidet ergo ez sectioni. // Coincidat ad m.
lcd pars scilicet toti. Quod est impossibile. // Coincidet ergo ez sectioni. // Coincidat ad m.
// Dico quod ad aliud punctum, quam m non coincidet.
// Si enim possibile est coincidat et apud n et agantur mx nb penes ag. // Eritque per praemissam ![]() emx aequale
emx aequale ![]() 124 enb pars toti: quod est impossibile. // Non igitur ez ad aliud, quam m punctum coincidet sectioni.
124 enb pars toti: quod est impossibile. // Non igitur ez ad aliud, quam m punctum coincidet sectioni.
// Vel sic agantur paralleli omp kng eritque per 34am primi Euclidis om aequalis kn sed ng maior125 quam mp ergo ![]() kng maius
kng maius ![]() omp quod est impossibile per 10am huius. Sunt enim aequalia. Quare non coincidet [A:44v] ez126 sectioni ad aliud quam m locum127: sicut proponebatur demonstrandum.
omp quod est impossibile per 10am huius. Sunt enim aequalia. Quare non coincidet [A:44v] ez126 sectioni ad aliud quam m locum127: sicut proponebatur demonstrandum.
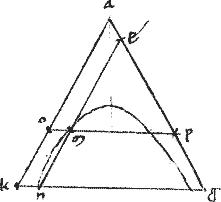
Manifestum est igitur ex prae senti propositione, et ex addita post tertiam huius libelli, quod omnis linea intra non coincidentes et alteri non coincidentium aequidistans deducta in uno tantum puncto coincidit hyperbolae128.