7^a Si conus plano secetur per axim, secetur autem et altero plano secante planum, in quo est basis coni per rectam ad rectos existentem vel basi trianguli per axim, vel eidem in rectam⁹⁵; ductae rectae a facta sectione in coni superficie, quam fecit secans planum, aequidistantes lineae trianguli⁹⁶ ad rectos basi⁹⁷, super communem sectionem cadent secantis plani et trianguli per axim: et productae ad alteram partem sectionis secabuntur per medium ad ipsa. Et si rectus est conus, linea in basi ad rectos erit communi sectioni plani secantis et trianguli per axim. Si autem scalenus, non semper ad rectos erit, sed tunc[A:4v] solum, quando planum per axim erit ad rectos basi coni .

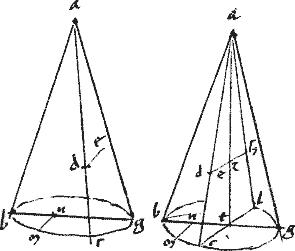
Conus, cuius vertex a basis autem bg circulus: secetur⁹⁸ plano per axem facientem, per 3^am triangulum abg. Secetur et altero plano, secante planum in quo est circulus bg per lineam de vel ad rectos existentem ipsi bg vel eidem in rectam⁹⁹: et faciat in superficie coni sectionem dze. Communis autem sectio secantis plani et trianguli abg sit linea zh et a quodam puncto periferiae dze utpote t ducatur recta tc aequidistans ipsi de.

Dico quod tc recta coincidet ipsi zh et producta ad alteram partem sectionis dze per medium secabitur a linea zh. Nam cum tc aequidistet ipsi dh catheto ad bg basim trianguli abg per axem¹⁰⁰ ducti: per praecedentem, producta coincidet triangulo abg et perinde ipsi rectae zh et extensa usque ad alteram partem superficiei conicae et perinde ad oppositam periferiam sectionis dze bifariam secabitur a triangulo abg in ipsa videlicet recta zh quae iacet in plano trianguli. Sic ostensa est prima propositi pars.

Sit autem abg conus rectus: tunc dico quod de linea ad rectos est ipsi zh. Tunc enim axis coni rectus est, per diffinitionem ad planum circuli bg et ideo per 18^am 11ⁱ Euclidis triangulum abg rectum est eidem circulo. Et ideo de linea, quae ad rectos est ipsi bg quae comunis sectio est trianguli et circuli ad rectos est ipsi triangulo abg et perinde ad rectos erit lineis in plano trianguli sibi conterminis: ideoque de ad rectos est ipsi zh quae fuit altera propositi pars.

Non aliter, si conus abg sit scalenus, modo triangulum abg rectum sit ad circulum bg ostendam de rectam esse ad ipsam zh. Si autem triangulum abg circulo bg non sit rectum: tunc solum de non erit ad rectos ipsi zh. Sit enim, si possibile est, tunc de ad rectos ipsi zh iam cum et ad rectos sit ipsi bg recta¹⁰¹ erit per 4^am 11ⁱ Euclidis ad planum trianguli abg. Quare, per 18^am eiusdem, circulus bg erit rectus ad triangulum abg¹⁰². Quod est contra hypothesim. Non igitur in eo casu de ad rectos est ipsi hz quod iam supererat demonstrandum.

[S:11]

Corollarium

Ex hoc autem manifestum est quod sectionis dze diameter est zh quoniam ductas aequidistantes cuidam rectae de bifariam dividit. Et quod possibile est a diametro zh aequidistantes quasdam per medium secari et non ad rectos¹⁰³.