6^a Si conus plano secetur per axim: relictumque sit quoddam⁸³ punctum in coni superficie, quod non sit in latere trianguli per axim: et ab ipso ducatur aequidistans cuidam rectae, quae est cathetus a circumferentia circuli [A:4r] ad basim trianguli; coincidet triangulo per axim: et ducta usque ad alteram partem superficiei, per medium secabitur a triangulo .

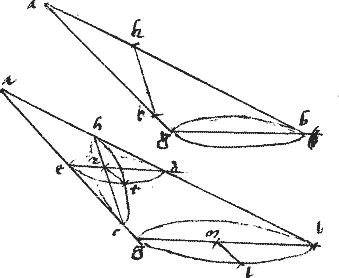
Conus, cuius vertex a basisque circulus bg secetur plano per axim, faciente, per 3^am84 triangulum abg et a puncto quopiam superficiei conicae, quod sit d ducatur linea⁸⁵ de aequidistans ipsi mn catheto quidem a periferia circuli ad bg basim trianguli⁸⁶.

Dico iam quod de producta coincidit plano trianguli abg et ad⁸⁷ alteram superficiei conicae partem extensa per medium secabitur a trianguli abg planitie. Coniungatur enim ad et producatur usque ad circumferentiam bmg ad punctum c. Sitque ct cathetus ad bg et perinde aequidistans ipsi mn et ideo, per 9^am 11ⁱ Euclidis aequidistans ipsi de. Eruntque, per 7^am praedicti ac ct de⁸⁸ rectae in eodem plano. Quare de producta occurret ipsi at exi[S:10]stenti in plano abg et perinde ipsi plano coincidet. Coincidat ad z puctum⁸⁹: et producatur dz donec in alteram partem occurrat superficiei conicae ad punctum h. [[Aio]]⁹⁰ quod et⁹¹ aequalis est dz ipsi zh producatur enim ct donec occurat periferiae ad l. Eruntque tria puncta a h l in superficie coni et in ipso plano acl et perinde in ipsa communi sectione secantis plani et conicae superficiei. Talis autem sectio per 3^am huius, recta linea est. Sunt igitur ahl puncta in eadem recta linea, quae sit ahl⁹². Et quoniam dzb ipsi ctl aequidistat⁹³; erit propter similitudinem triangulorum, sicut at az sic et⁹⁴ ct dz et tl zh. Aequalis autem est per 3^am 3ⁱⁱ Euclidis ct ipsi tl. Aequalis ergo est per 14^am 5ⁱ et dz ipsi zh. Quod demonstrandum supererat.