* LEMMA

Si curvam lineam recta subtendat: omnis autem cathetus a curva in rectam possit rectangulum, quod sub segmentis rectae⁵³; curva linea circuli periferia est, cuius diameter⁵⁴ recta ipsa.

Curvam lineam abg subtendat recta⁵⁵ ag et omnis cathetus a curva in rectam ut pote bd possit ^um sub segmentis rectae, ut sub ipsis ad dg contentum.

Dico quod Abg flexa circulus est.

Secetur enim ag bifariam in puncto e et connectatur eb.

Eruntque per 5am 2i Euclidis ad dg ed simul aequalia to eg.

Cumque sit per hypothesim db aequale ad dg⁵⁶.

Erunt iam pridem ed db simul aequalia to eg.

Sed per penultimam primi Euclidis eadem aequalia⁵⁷ eb.

Igitur eg eb⁵⁸ aequalia⁵⁹: et perinde rectae eg eb⁶⁰ aequales.

[A:3v] Similiter ostendam quod omnes rectae a puncto e ductae⁶¹ ad flexam lineam abg singulae sunt aequales ipsi eg quare, per diffinitionem abg curva circulus⁶² est: sicut⁶³ proponitur.

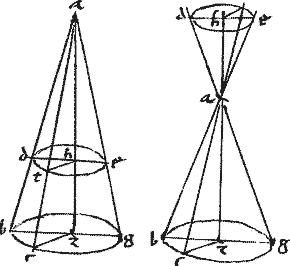
5^a Si conus scalenus plano secatur per axim ad rectos⁶⁴ basi: secetur autem et altero plano ad rectos triangulo per axim⁶⁵, auferente autem ad verticem triangulum simile quidem per axim triangulo, subcontrarieque⁶⁶ positum; sectio circulus est. Vocetur autem talis sectio subcontraria. .

[S:9] Conum scalenum, cuius vertex a basis bg circulus: secet planum per axem et rectum ad bg circulum; ac faciens, per 3^am abg triangulum. Item secet et conum aliud planum ipsi abg triangulo rectum: cuius cum triangulo communis sectio sit recta hc ita ut triangulum ahc⁶⁷ ablatum ad verticem simile sit triangulo agb subcontrarie vero⁶⁸ positum, hoc est ut angulus ach aequalis sit angulo abg et reliquus reliquo. Faciatque tale planum in superficie conica periferiam htc.

Dico iam quod htc⁶⁹ sectio circulus est. Capiantur enim puncta quaedam in periferiis htc blg quae sint⁷⁰ t l a quibus ad planum trianguli abg catheti ducantur⁷¹: cadent utique ad communes sectiones planorum: cadant ergo, sintque tz lm quae per 6^am 11ⁱ Euclidis erunt aequidistantes. Sit ergo dze ipsi bg aequidistans.

Eritque per 15^am 11 Euclidis planum ezt aequidistans circulo glb conicae scilicet basi. Quare per praecedentem planum ezt circulum, qui est etd facit in cono. Et ideo per 35^am 3ⁱⁱ⁷² Euclidis, tz aequum est dz ze⁷³.

Verum propter similitudinem triangulorum dzb cze ut quae⁷⁴ sint invicem aequiangula ex hypothesi. Sic quidem⁷⁵ dz cz sic est zh ze.

Quare per 15^am sexti Euclidis dz ze⁷⁶ aequale est ^lo cz zh ⁷⁷ fuit autem tz ⁷⁸ aequum ^lo dz ze ⁷⁹.

Igitur et⁸⁰ tz aequum erit ^lo cz zh ⁸¹. Similiter ostendam omnem⁸² cathetum a periferia htc in recta hc posse ^um sub segmentis ipsius hc comprehensum: et ideo per praemissum lemma, sectionem htc circulum esse, cuius diameter ch. Quod erat demonstrandum.