LEMMA
In circulo abg sit ab chorda: et ag diameter: data ratio de ![]() ez. Oportet a diametro ad periferiam ducere lineam924 penes ipsam ab ut pote ro ita, ut
ez. Oportet a diametro ad periferiam ducere lineam924 penes ipsam ab ut pote ro ita, ut ![]() ro
ro ![]()
![]() arg sit sicut de
arg sit sicut de ![]() ez.
ez.
Ponatur ipsi de aequalis zh et eh bifariam secetur apud t et a circuli cen[S:48]tro
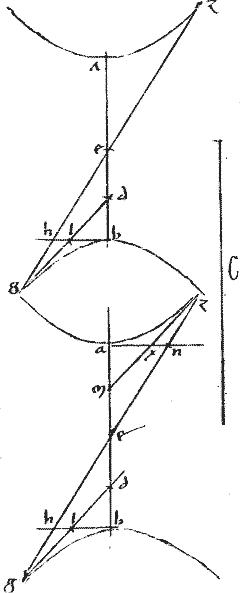
c ducatur kathetus ad ab usque periferiam ad l. Et agatur lm penes ipsam ab et coincidat ipsi ca apud m. Sitque sicut tz ![]() zh sic lm
zh sic lm ![]() mn. Ponaturque ipsi ln aequalis lx. Et coniungantur nc cx et productae [A:36r] coincidant periferiae apud o p. Et op coniuncta secet ipsam cg apud r.
mn. Ponaturque ipsi ln aequalis lx. Et coniungantur nc cx et productae [A:36r] coincidant periferiae apud o p. Et op coniuncta secet ipsam cg apud r.
// Et quoniam tz ![]() zh sicut925 lm
zh sicut925 lm ![]() mn.
mn.
Et conversim zh ![]() zt sicut mn
zt sicut mn ![]() lm.
lm.
Et coniunctim ht ![]() tz sicut nl
tz sicut nl ![]() lm.
lm.
|
|
|
|
|
|
Ideo ex aequali, quandoquidem zh ![]() tz
tz ![]() th
th ![]() ze continuant tres rationes, quas continuant mn
ze continuant tres rationes, quas continuant mn ![]() lm
lm ![]() ln
ln ![]() mx singulas singulis aequales; erit zh sive de
mx singulas singulis aequales; erit zh sive de ![]() ez sicut mn
ez sicut mn ![]() mx.
mx.
Cumque, propter angulos ad l rectos, et lineas926 ln lx et ipsas oc cp927 aequales ipsae928 nx op sint paralleli929.
Propterea ![]()
![]() cmn cro sunt invicem aequiangula: itemque ipsa
cmn cro sunt invicem aequiangula: itemque ipsa ![]()
![]() cmx crp invicem aequiangula.
cmx crp invicem aequiangula.
Quare, per 4am 6i Euclidis mc ![]() cr sicut930 mn
cr sicut930 mn ![]() ro et sicut mx
ro et sicut mx ![]() pr. Et permutatim nm
pr. Et permutatim nm ![]() 931 mx et ideo de
931 mx et ideo de ![]() ez sicut or
ez sicut or ![]() rp932 et ideo per primam 6i sicut
rp932 et ideo per primam 6i sicut ![]() or
or ![]()
![]() orp933.
orp933.
Sed, per 33am tertii ![]() orp aequale est
orp aequale est ![]() arg igitur sicut
arg igitur sicut ![]() or
or ![]()
![]() arg sic934 de
arg sic934 de ![]() ez. Estque or penes ipsam ab.
ez. Estque or penes ipsam ab.
Itaque or est linea, quae ducenda proponitur.
54a Duabus datis lineis terminatis ad rectos invicem; invenire circa diametrum alteram ipsarum coni sectionem vocatam ellipsin935, in eodem plano lineis936, cuius summitas sit punctum, quod est ad rectum angulum applicatae autem a sectione ad diametrum in dato angulo possint id, quod adiacentia rectangula ad alteram lineam937, latitudinem habentia receptam sub ipsa ad summitatem sectionis, deficientia specie simili et similiter posito938 contento sub datis lineis.
Sint ad rectos datae ba ag quarum maior ab. // Datusque angulus primum939 rectus.
// Oportet in subiecto plano bag ellipsim describere: cuius diameter sit ab. // Summitas a. // Recta diametros ag. // Et ordinatae940 ad datum angulum applicatae.
Exurgat ex ab planum rectum ad subiectum, in quo circuli peripheria adb describatur bifariam secta apud d. Et coniungantur ad db941.
Sitque ipsi ag aequalis ax.
Et penes ipsam db agatur xo942. Et penes ipsam ab agatur oz.
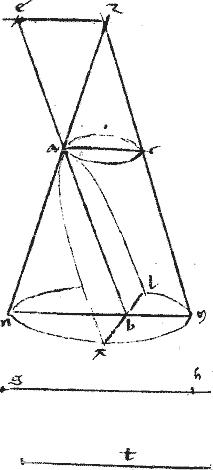
Et con[A:36v]iungatur dz. // Quae producta coincidat ipsi ba apud e.
// Et coniungantur az zb et producantur. Et a puncto utcunque943 relicto in za quod sit h agatur penes de linea ht coincidens ipsi ab apud c ipsique zo apud l.
// Eritque, per 26am tertii Euclidis angulus abd944 aequalis angulo dzb.
// Et quoniam945, per 16am primi Euclidis angulus eza exstrinsecus aequalis est angulis zad zda sibi intrinsecus oppositis: et ideo aequalis angulis zbd zba per 26am tertii: et ideo toti angulo abd et ideo ipsi angulo dzb. Atque, per 29am primi, angulus eza aequalis angulo zht coalterno: et angulus dzb aequalis angulo zth coalterno. Propterea anguli zth zht sunt invicem aequales. Quare per 6am primi Euclidis hz zt lineae aequales.
Describatur itaque circulus htn rectus ad ![]() thz.
thz.
Et intelligatur conus, cuius basis circulus ipsae htn vertex vero z qui rectus erit propter latera hz zt aequalia.
Et quoniam tam cir[S:49]culus htn quam subiectum planum rectum est ad ![]() thz ideo, per 19am undecimi Euclidis circuli htn subiectique plani sectio communis, quae sit recta cm recta erit ad planum , quod per946 thz.
thz ideo, per 19am undecimi Euclidis circuli htn subiectique plani sectio communis, quae sit recta cm recta erit ad planum , quod per946 thz.
Et perinde ipsa cm et omnis ei parallelus recta947 erit, hoc est ad rectos ipsis948 ac ch.
Itaque quoniam subiectum planum rectum949 ad ![]() thz quod per axem coni et coincidens hz zt lateribus coni secat conum tzh.
thz quod per axem coni et coincidens hz zt lateribus coni secat conum tzh.
Ideo, per 13am huius, sectio facta in cono, cuius diameter ab ellipsis est, cuius summitas a et ordinatae950 ductae ad rectos diametro.
Et quoniam de ![]() ez per primam sexti , sicut951
ez per primam sexti , sicut951 ![]() dez vel
dez vel ![]() bea952 per 35am tertii
bea952 per 35am tertii ![]()
![]() ez et sic est da
ez et sic est da ![]() ao ba953
ao ba953 ![]() ax per 2am sexti et ba
ax per 2am sexti et ba ![]() ag.
ag.
|
|
Quare, per 13am huius, ellipseos956 cuius transversa957 ba rectum latus est ag. Factum est ergo, quod faciendum proponitur.
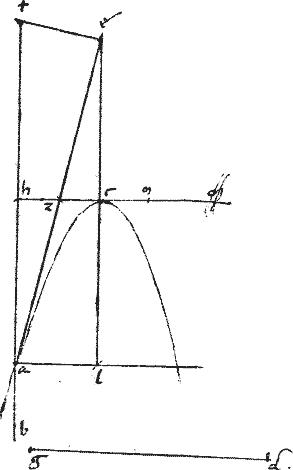
Iisdem subiectis, sit ab minor, quam ag. // Et oporteat958 circa ab diametrum, ellipsim describere, cuius recta sit ag.
// Secetur ab bifariam apud d et ducatur edz ad rectos ab. // Sitque ez media proportionalis inter ba ![]() 959 ag et apud d bifariam secta. // Item zh penes ipsam ab. // Sitque ut ga
959 ag et apud d bifariam secta. // Item zh penes ipsam ab. // Sitque ut ga ![]() ab [A:37r] sic ez
ab [A:37r] sic ez ![]() zh. // Quare ez maior960, quam zh. // Et quoniam ag961
zh. // Quare ez maior960, quam zh. // Et quoniam ag961 ![]() ez
ez ![]() ab sunt in proportione continua: ideo, per 17am sexti Euclidis ag
ab sunt in proportione continua: ideo, per 17am sexti Euclidis ag ![]() ab et ideo ez
ab et ideo ez ![]() zh sicut962
zh sicut962 ![]() ez
ez ![]()
![]() ab et sicut
ab et sicut ![]() dz
dz ![]()
![]() da963.
da963.
// Describatur igitur, ut prius, ellipsis, cuius diameter ez recta vero964 zh. // Quae sit azbe. // Ibit enim per a quoniam ![]() zde
zde ![]()
![]() da sicut965 ez
da sicut965 ez ![]() zh per conversionem corollarii 13ae huius. Ibit etiam per b quandoquidem ad db aequales.
zh per conversionem corollarii 13ae huius. Ibit etiam per b quandoquidem ad db aequales.
// Et quoniam ga ![]() ab sicut966
ab sicut966 ![]() dz
dz ![]()
![]() da et conversim: ideo, per eiusdem corollari conversionem, recta sectionis est ag.
da et conversim: ideo, per eiusdem corollari conversionem, recta sectionis est ag.
// Vel argue, per conversionem 2i corollarii: quoniam ez secunda diametros media proportionalis fuit inter ba primam diametrum et ipsam az967 sitque ba transversa; erit az968 recta diametros969. // Rursus ergo factum, quod proponitur.
SCHOLIUM
Attendendum970 in praesenti descriptione, quod sicut ba transversa diametros in ellipsi971 habet rectam suam ag. // Ita et posita ez transversa sortitur ipsam zh rectam. // Unde, sicut patuit in 15a huius, eiusque corollario972 , ag ![]() ez
ez ![]() ba sunt in proportione continua: itemque ez973
ba sunt in proportione continua: itemque ez973 ![]() ba
ba ![]() zh continue proportionales974: quare, et ag
zh continue proportionales974: quare, et ag![]() ez
ez![]() ba
ba ![]() zh quatuor sunt in proportione continua.
zh quatuor sunt in proportione continua.
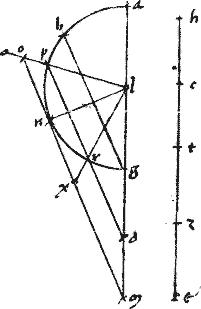
Sed non sit iam datus angulus rectus, utpote975 bad. Caeteris, ut ante, admissis. // Secetur tunc ab per medium apud e. // Et super ae diametro describatur semicirculus aze. // Et ducatur zh penes ad ita, ut ![]() zh
zh ![]()
![]() ahe sit sicut ga
ahe sit sicut ga ![]() ab quemadmodum docet976 lemma praemissum. // Et coniungantur az ze et producantur. // Sitque ipsarum de ez media proportionalis et ipsique977 et aequalis sit ec.
ab quemadmodum docet976 lemma praemissum. // Et coniungantur az ze et producantur. // Sitque ipsarum de ez media proportionalis et ipsique977 et aequalis sit ec.
// Et ![]() tzl aequale sit978
tzl aequale sit978 ![]() az. // Et coniungatur cl at979. // Et penes ipsam az agatur ipsa ntm coincidens ipsis ba cl apud n m.
az. // Et coniungatur cl at979. // Et penes ipsam az agatur ipsa ntm coincidens ipsis ba cl apud n m.
// Quibus peractis, sicut antea, describatur ellipsis, cuius diameter ct recta vero tm et ordinate ductae ad rectos ipsi tc quae sit atbc980. Ibit enim per a ex conversione corollarii 13ae huius, quandoquidem ![]() az aequale est
az aequale est ![]() tzl ibit et, per b quoniam ae eb aequales981. Centrumque982 sectionis erit e diametrique ab ct. // Et ipsa da tanget sectionem, per conversam 37ae983 huius, quoniam scilicet984
tzl ibit et, per b quoniam ae eb aequales981. Centrumque982 sectionis erit e diametrique ab ct. // Et ipsa da tanget sectionem, per conversam 37ae983 huius, quoniam scilicet984 ![]() dez aequale985
dez aequale985 ![]() et. // Quare, per 47am ab secabit actas in sectione ipsi ad parallelos, et ideo ad angulum datum bad ordinate ductas, singulas bifariam, et perinde diameter erit.
et. // Quare, per 47am ab secabit actas in sectione ipsi ad parallelos, et ideo ad angulum datum bad ordinate ductas, singulas bifariam, et perinde diameter erit.
// Et quoniam ga ![]() ab sicut986
ab sicut986 ![]() zh
zh ![]()
![]() ahe et ratio ga
ahe et ratio ga ![]() ab [A:37v] componitur ex rationibus ga
ab [A:37v] componitur ex rationibus ga ![]() duplam da et duplae da
duplam da et duplae da ![]() ab vel da
ab vel da ![]() ae vel zh [S:50]
ae vel zh [S:50] ![]() he.
he.
|
|
|
Communis auferatur ratio zh ![]() he.
he.
|