[S:46]

Lemma

Esto semicirculus abg. // Data ratio ez zh. // Oportet ipsi gb parallelum⁸⁶² ducere, utpote⁸⁶³ rd coincidentem ipsi ag productae, ita ut rd adg sit sicut ez zh.

Ducatur a centro l kathetus⁸⁶⁴ ad ipsam bg usque ad periferiam ln⁸⁶⁵. // Et nm penes ipsam bg quae, per 15^am 3ⁱⁱ Euclidis tanget circulum. // Deinde sit [A:34v] ipsi ez aequalis zt. // Item th apud c bifariam secta.

// Et sicut zt tc sic sit⁸⁶⁶ mx xn. // Ipsique xn aequalis sit no. // Et coniungantur lx lo secantes periferiam⁸⁶⁷ apud r p. // Et coniungatur prd.

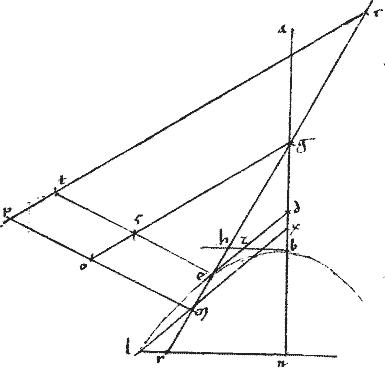
// Itaque propter lineas xn no aequales, aequidistat prd ipsi mo ita ut ipsarum om pd sint proportionalia, per 2^am 6ⁱ Euclidis⁸⁶⁸.

// Cumque sit zt tc sicut mx xn. // Et ct th sicut nx xo.⁸⁶⁹ // Erit ex aequali⁸⁷⁰ zt th sicut mx xo. // Et conversim ht tz sicut ox xm. // Et coniunctim⁸⁷¹ hz zt vel ze sicut⁸⁷² om mx atque ideo sicut⁸⁷³ pd dr.

// Sed⁸⁷⁴ pd dr sicut⁸⁷⁵ pdr dr per primam sexti Euclidis. // Cumque per 35^am tertii adg aequale sit pdr erit et pd dr sicut adg dr. // Igitur adg dr sicut⁸⁷⁶ hz ze. // Et conversim dr adg sicut⁸⁷⁷ ez zh. // Itaque pd est linea, quae ducenda⁸⁷⁸ proponitur.

53^a. Duabus datis lineis terminatis ad rectos invicem, altera producta in eodem recto angulo;⁸⁷⁹ invenire in producta coni sectionem nuncupatam hyperbolen in eodem plano lineis,⁸⁸⁰ ut productae exordium centrum sit⁸⁸¹ sectionis, summitas autem punctum ad angulum: quae autem⁸⁸² ducitur a sectione ad diametrum angulum faciens aequalem dato possit id, quod adiacens rectangulum ad alteram lineam, latitudinem habens receptam sub applicata ad summitatem, excedens specie simili et similiter posita sub lineis a principio.

Sint ad rectos datae ab bg. // Et producatur ab usque ad d. // Angulusque datus primum rectus⁸⁸³.

// Oportet invenire hyperbolen in plano abg cuius transversa diametros ab. Recta vero sit bg. Summitas [[quae]]⁸⁸⁴ punctum b. Et ordinate ductae a sectione ad bd sint ad datum angulum applicatae⁸⁸⁵.

// Exurgat ex ab planum rectum ad subiectum planum: et in ipso circa ab circulus describatur aebz ipsa⁸⁸⁶ el ipsam ab bifariam et ad rectos apud c secante et perinde diametro [[exente]]⁸⁸⁷ ita ut⁸⁸⁸ ec cl maior non sit, quam ab bg.

// Itaque si ec cl sit sicut ab bg capiatur l punctum. // Sin vero, sit ec cm⁸⁸⁹ sicut ab bg et capiatur m punctum. // Et ducatur mz penes⁸⁹⁰ ipsam ab. // Et coniungantur az ez zb. // Et agatur bx penes⁸⁹¹ ez. //

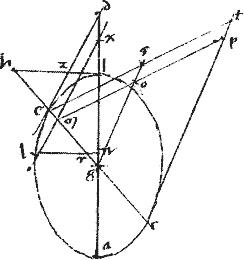
// Eritque per 26^am 3ⁱⁱ angulus aze aequalis angulo ezb quandoquidem aequales periferias subtendunt.

// Sed per 29^am primi Euclidis angulus aze ipsi zxb angulus autem ezb angulo zbx aequalis est.

// Igitur anguli zxb zbx invicem aequales: [A:35r] // Et ideo, per 6^am primi Euclidis ipsae bz zx aequales⁸⁹².

// Itaque intelligatur conus: cuius vertex z basis vero circulus circa diametrum bx rectus ad bzx. Eritque rectus conus, quandoquidem bz zx aequales⁸⁹³.

// Deinde producantur zb zx mz ab totaque conica superficies: quae secetur plano, quod parallelum sit ipsi bx circulo. Sitque sectio circulus per 4^am huius, ptr⁸⁹⁴ cuius diameter th.

// Eritque cir[S:47]culus ptr sicut circulus bx rectus ad zht. // Quare per 19^am 11ⁱ Euclidis pdr linea, quae communis sectio est subiecti plani et circuli ptr recta erit ad idem zht et ideo ad ipsas th db.

// Itaque, quoniam sectionis pbr quam subiectum planum rectum ad zht in cono facit, diameter⁸⁹⁵ db coincidit⁸⁹⁶ lateri coni hz producto supra verticem apud a. // Ideo, per 12^am huius sectio pbr hyperbole⁸⁹⁷ est: cuius diameter⁸⁹⁸ ab vertex b et ordinate ductae ad rectos diametro. // Et quoniam ab⁸⁹⁹ bg sicut⁹⁰⁰ ec cm et ideo sicut [[en]] [[nz]] per 2^am sexti Euclidis ideo et⁹⁰¹ sicut enz nz⁹⁰², per prima eiusdem sexti.

// // Sed enz aequale est anb per 34^am. tertii:⁹⁰³: igitur ab bg sicut⁹⁰⁴ anb nz.

// Producta vero zo penes ipsam bd anb nz

ratio componetur ex rationibus an nz ad dh zo oh bn nz bd dt zo ot 905

propter linearum aequedistantiam et similitudinem.

// Igitur et ratio ab bg componetur906 ex rationibus zo oh zo ot

ex quibus componitur ratio zo hot. // Quare ab bg sicut⁹⁰⁷ zo ho. //⁹⁰⁸ Cumque zo aequedistet ipsi ad. // Erit per 12^am huius ab transversum: bg vero rectum sectionis pbr hyperboles latus.

// Factum ergo⁹⁰⁹, quod proponebatur faciendum.

Sed non sit iam datus angulus rectus: sintque datae lineae ab ag. // Datusque angulus bat.

// Oportet itaque describere hyperbolen, cuius diameter ab. // Recta vero ag. // Ordinate autem ductae ad angulum tab applicandae.

// Secetur ab bifariam in puncto d. // Et circa ad describatur semicirculus azd. // Et penes ipsam at ducatur zh coincidens ipsi da productae in h. [A:35v] Ita ut zh dha sit sicut ag gb⁹¹⁰ sicut⁹¹¹ lemma praemissum docet⁹¹². // Et coniungatur ztd. // Et ipsarum zd dt media proportionalis sit dl. // Ponaturque ipsi ld aequalis dc et lzm

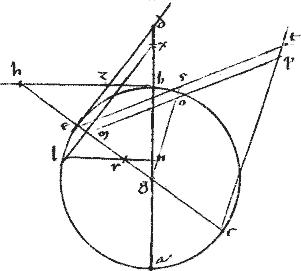
aequale⁹¹³ az. // Et coniungatur cm. // Et nlx ad rectos ipsi dz. // Quibus peractis, describatur, ut prius, hyperbole⁹¹⁴, cuius diameter⁹¹⁵ cl recta diameter⁹¹⁶ ln summitas l quae hyperbole⁹¹⁷ sit al. // Ibit enim per a quandoquidem az potest lzm ut patet per 12^am huius.

// Eritque at tangens sectionem, per conversam 37ae huius quoniam zdt dl aequalia918.

Cumque ab eat per d centrum secabit actas in sectione ipsi ta tangenti parallelos, et⁹¹⁹ ideo ad angulum bat ordinate ductas, bifariam singulas, per 47^am huius , et perinde ipsa ab diameter erit sectionis.

// Et quoniam ga duplam ipsius ad hoc est ab⁹²⁰ sicut⁹²¹ zh dha. //

Atque ratio ga ab componitur ex rationibus

ga duplam ipsius at duplae at ab vel at ad vel zh hd

.

// Itemque ratio zh dha componitur ex rationibus zh hd zh ha .

// Propterea ratio composita ex rationibus zh hd zh ha

aequalis est rationi compositae ex rationibus ga duplam at zh hd .

// Communis auferatur ratio zh hd et supererit ga duplam at sicut zh ha verum zh ha sicut⁹²² oa ax propter similitudinem. Igitur oa ax sicut⁹²³ ga duplam at.

// Quare per 50^am huius ipsa ag recta diametros est hyperboles al.

// Rursus ergo factum est: quod faciendum proponebatur.