50^a Si hyperbolen, vel ellipsin, vel circuli periferiam linea tangens coincidat diametro: et per tactum et centrum linea producatur: et a summitate ducta linea ordinate applicata coincidat ductae lineae per tactum et centrum: et factum sit,⁷⁶⁹ ut portio tangentis inter applicatam et tactum ad portionem ductae per centrum et tactum, quae inter tactum et applicatam; sic⁷⁷⁰ assumpta quaedam linea ad duplam tangentis; quae a sectione ducitur ad ductam per centrum et tactum, aequidistans tangenti, poterit id, quod quaedam superficies rectangula adiacens ad lineam assumptam et latitudinem habens receptam sub ipsa usque ad tactum, in hyperbole quidem excedens specie simili contento sub dupla eius, quae inter centrum et tactum et sub assumpta⁷⁷¹ linea, in ellipsi autem et circulo deficiens.

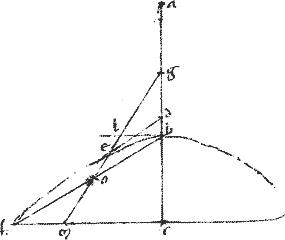
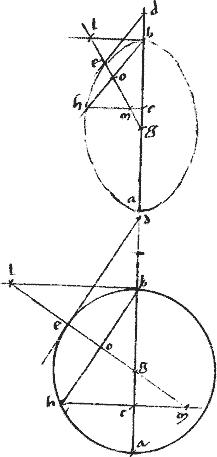
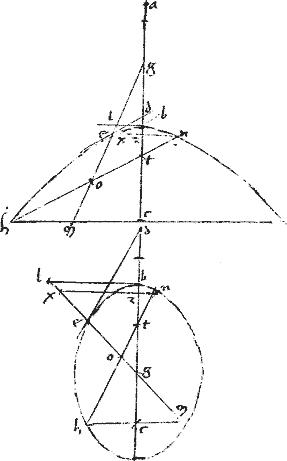
Sit hyperbole, vel ellipsis, vel circulus, cuius diameter ab. // Centrum g. // Tangens de. // Et ge producatur utroversum, ut ipsi⁷⁷² eg⁷⁷³ aequalis sit gc⁷⁷⁴. // Ordinate ducta bzh coincidens⁷⁷⁵ ipsi⁷⁷⁶ quidem de ad signum z ipsique ge apud h. // Sitque sicut ze eh sic et duplam ipsius ed. // Ponaturque et ad rectos⁷⁷⁷ ipsi eg. // Et tc coniuncta producatur. // Et per relictum quoddam⁷⁷⁸ punctum in sectione, ut l agatur penes ed tangentem linea lmx coincidens ipsi ge productae apud m et diametro ab apud x. // Item penes ipsam bh ducatur lrn coincidens ipsi⁷⁷⁹ ge productae apud r ipsique diametro ab apud n. //

// Demum penes ipsam et ducatur mp coincidens ipsi at⁷⁸⁰ productae apud p.

// Dico iam quod lm aequale est emp quod, quidem emp⁷⁸¹ adiacet ad lineam assumptam et⁷⁸² sub latitudine em recepta ab lm ad tactum et in hyperbola excedit ipsam et⁷⁸³ specie simili ^lo cet. In ellipsi vero et circulo deficit.

// Hoc est, quod transversa diametro existente ce recta erit et.

// Agatur enim penes ipsam cp recta gso. // Et quoniam eg aequalis est ipsi gc

atque, per 2^am 6ⁱ Euclidis sicut eg gc sic es st ideo es aequalis st. // Et quoniam ze eh sicut⁷⁸⁴ et duplam ipsius ed estque es 1/2 ipsius et. Ideo ze eh sicut es ed.

// Et quoniam ze eh sicut lm mr propter zeh lmr similitudinem: ideo [S:43] lm mr sicut⁷⁸⁵ es⁷⁸⁶ ed.

// Et, quoniam, per 43^am huius, in hyperbola rng aequale gbh lnx et ideo gde lnx cum per additam post 42^am gbh gde sint aequalia. // In ellipsi vero et circulo, quoniam gbh sive gde aequale est rng lnx. [A:32r] // Ideo, communibus ablatis, in hyperbola⁷⁸⁷ quidem egd cum rmxn. // In ellipsi autem et circulo mxg supererit lmr aequum medx.

// Sed anguli ad m contrapositiaequales⁷⁸⁸: ergo lmr aequum ^mo789 facto ex em

in aggregatum ipsarum ed mx .

// Quandoquidem illud duplum⁷⁹⁰ lmr hoc autem duplum est ^mi medx⁷⁹¹.

// Et quoniam mg ge sicut⁷⁹² mx ed itemque⁷⁹³ sicut mo es. // Ideo sicut mo es sic⁷⁹⁴ est mx ed propter linearum aequedistantiam et similitudinem.

// Et coniunctim mo es es sicut mx ed ed.

// Et permutatim mo es mx ed sicut⁷⁹⁵ es ed.

// Sed, per primam 6ⁱ Euclidis mo es mx ed sicut⁷⁹⁶

mo es mx ed em em

fuitque es ed sicut ze eh et sicut lm mr et per primam 6ⁱ sicut lm lmr.

// Igitur lm lmr sicut mo es mx ed em em .

8 //

// 9 Ergo

et lm aequum erit mo es em .

// Sed mo es em aequale est emp. Namque797 emp

sit ex em in dimidium aggregati ipsarum etmp. // Quod quidem dimidium est congeries ipsarum mo es.⁷⁹⁸

Igitur⁷⁹⁹ emp aequale est lm.

Quod fuit demonstrandum.

Similiter ostendemus, quod omnis⁸⁰⁰ a puncto quovis sectionis penes de tangentem ducta ad cgm⁸⁰¹ diametrum linea poterit contentum sub et linea et sub recepta ex diametro cge ad tactum, in hyperbola quidem excedens specie simili contento sub [A:32v]ipsis ce et in ellipsi autem et circulo deficiens. Atque ideo, cum sit ce transversa diameter, erit et recta diametros⁸⁰², ad quam videlicet possunt ordinate ductae ad transversam in hyperbola, ellipsi et circulo.