49^a Si parabolen linea tangens coincidat diametro: et per tactum ducatur aequedistans⁷³⁸ diametro: et a summitate ducatur ordinate⁷³⁹ applicata⁷⁴⁰: et factum sit⁷⁴¹, ut portio tangentis inter applicatam et tactum ad portionem aequidistantis inter tactum et applicatam; sit⁷⁴² assumpta quaedam linea ad duplam tangentis; quae a sectione ducitur ad ductam per tactum aequedistantem diametro, aequedistans tangenti poterit contentum rectangulum sub assumpta linea et sub recepta usque ad tactum ex ea, quae penes diametrum.

Sit parabole, cuius diameter mbg. // Tangens gd. // Punctum tactus d. // Ipsa zdn penes ipsam bgm. // Ordinate ducta bz secans ipsam gd apud e. // Sitque sicut ed dz sic linea H⁷⁴³ duplam dg. // Et per quoddam⁷⁴⁴ relictum in sectione punctum ut c agatur penes ipsam dg linea clp ipsi zd apud l diametroque apud p coincidens.

// Dico iam quod cl aequale est H dl⁷⁴⁵ hoc est, quod diametro existente dl recta erit H⁷⁴⁶ linea.

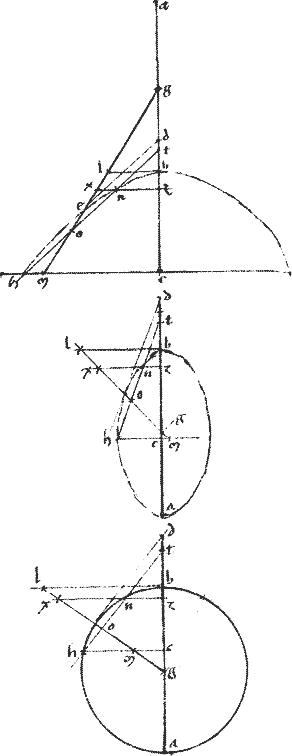
// Ducantur enim ordinate ad diametrum gbm⁷⁴⁷ ipsae dx cm lineae: cui dl coincidat apud l⁷⁴⁸.

// Eritque, per 35^am huius , gb ipsi bx et ideo ipsi zd aequalis. // Quare et ebg edz invicem aequalia.

// Communis ponatur debmn figura: eritque dgmn aequale zm.

// Sed per 42^am huius zm aequum cpm. // [S:42] Igitur cpm et dgmn aequalia⁷⁴⁹.

// Commune auferatur lpmn et relinquetur cln aequale ^mo lg. // Et, quoniam anguli ad l contrapositi aequales⁷⁵⁰ ideo cln duplum est ad ldg.

// Et quoniam ed dz sicut⁷⁵¹ cl ln propter similitudinem . // Ideo cl ln sicut⁷⁵² H⁷⁵³ duplam dg. // Sed per primam 6ⁱ cl cln sicut⁷⁵⁴ cl ln. // Et H dl gdl sicut⁷⁵⁵ H⁷⁵⁶ duplam gd.

// Igitur H dl gdl⁷⁵⁷ sicut⁷⁵⁸ cl cln.

// Et permutatim sicut H dl cl⁷⁵⁹ sicut⁷⁶⁰ gdl cln. Sed gdl aequale fuit cln.

// Ergo et H dl ⁷⁶¹ aequale est cl⁷⁶². // Quod erat demonstrandum.

[A:31v] Similiter ostendemus quod omnis⁷⁶³ a puncto quovis sectionis penes⁷⁶⁴ dg tangentem ad dl diametrum ducta linea⁷⁶⁵ poterit contentum sub H⁷⁶⁶ linea et sub recepta ex diametro ad tactum usque rectangulum: atque ideo, cum sit dl diameter transversa, erit H⁷⁶⁷ recta diametros⁷⁶⁸, ad quam possunt ordinate ductae ad transversam in parabola.