51^a. Si alteram contrapositarum linea tangens coincidat diametro: et per tactum et centrum producatur quaedam linea usque ad alteram sectionem: et a summitate linea ducatur ordinate applicata⁸⁰³ et coincidat lineae per tactum et centrum ductae: et fiat,⁸⁰⁴ ut portio tangentis inter applicatam et tactum ad portionem ductae per tactum et centrum, inter tactum et applicatam; sic⁸⁰⁵ linea quaedam assumpta ad duplam tangentis; quae in altera sectionum ad ductam per tactum et centrum linea ducitur aequedistans tangenti, poterit adiacens rectangulum ad lineam assumptam, latitudinem habens receptam sub ipsa ad summitatem, excedens specie simili contento sub ea, quae est inter contrapositas, et sub assumpta linea.

Sint contrapositae: // quarum diameter ab. // Centrum e. // Tangens sectionem b linea gd. // Et coniungatur ge producaturque donec coincidat alteri sectioni per 31^am huius, apud z. // Ordinate ducta blh coincidens ipsi dg apud l ipsique eg apud h. // [S:44] Et fiat, ut lg gh⁸⁰⁶ sic assumpta quaedam linea c ⁸⁰⁷ duplam ipsius dg. // Eritque per praecedentem, ut, quae in sectione bg sunt, aequedistantes ipsi dg ad lineam eg ductae possint id, quod superes⁸⁰⁸ adiacentes⁸⁰⁹ ad assumptam c⁸¹⁰ latitudinem habentes⁸¹¹ receptam sub ipsis ad tactum usque excedentes⁸¹² specie simili, ei quod sub gz c⁸¹³ nam gz dupla est ipsius⁸¹⁴ ge.

// Dico iam quod in sectione az id⁸¹⁵ idem contingit.

// Ducatur enim per z linea mz tangens sectionem az.

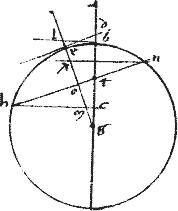
// Et ordinate applicetur axn ipsi mz apud x ipsique ez apud n coincidens. // Eritque, per additam post 43^am, huius mz tangens, ipsi gd tangenti aequalis et aequidistans⁸¹⁶: item me ipsi ed aequalis: unde et am aequalis ipsi db. // Quo sit ut respondentes lineae hinc et inde singulae singulis sint aequales. // Itaque cum sit lg gh sicut c duplam ipsius gd. // Erit et xz zn sicut c duplam zm.

[A:33r] // Quando igitur hyperbole est az cuius diameter ab. // Tangens autem mz et ordinate ducta an. // Et est ut xz zn sic c duplam ipsius zm iam, per praecedentem, quaecunque intra sectionem penes ipsam zm ducentur⁸¹⁷ ad lineam ez [[poterunt]] id, quod⁸¹⁸ contentum sub c linea et recepta sub ipsis⁸¹⁹ usque ad tactum z excedens specie simili ei, quod sub gz c⁸²⁰ continetur.

Manifestum est ergo quod cum contrapositarum communis sit transversa diameter gez erit et earumdem recta diametros⁸²¹ c ad quam videlicet possunt ordinate ductae ad transversam in utravis sectione contrapositarum.

Corollarium

Demonstratis autem his, simul manifestum est, quod in parabole unaquaeque ductarum penes diametrum linearum ex generatione diameter erit. In hyperbola autem, ellipsi, circulo et contrapositis unaquaeque per centrum ductarum linearum. Et quod in parabole ductae ad unamquamque diametrum penes tangentem poterunt id quod adiacentia, modo praedicto, ad ipsam rectangula: in hyperbole autem et contrapositis, id, quod adiacentes, ut dictum est, ad ipsam superficies et excedentes eodem⁸²² specie. In ellipsi autem et circulo, id, quod adiacentia⁸²³ ad ipsam et deficentia eodem⁸²⁴ specie. Et quod quaecumque demonstrata sunt circa sectiones contingentia⁸²⁵ comparatis principalibus diametris, et aliis diametris assumptis, eadem accident.

//

Scholium

// Principales diametros sectionum intellige communes sectiones triangulorum per axim coni ductorum et planorum facientium in superficie conica sectiones: ad quas quidem diametros ordinate ductae nunc sunt ad rectos et tunc ipsae diametri dicuntur axes: nunc non⁸²⁶ ad rectos, et tunc non sunt axes. Quaecumque ergo demonstrata sunt, circa sectiones, ita demonstrata sunt, ut diametri simpliciter diametri, non semper axes intelligantur⁸²⁷. Cum ordinate ductae ut in 7^a patuit, non semper ad rectos sint diametris. Unde et in his sex immediate praemissis propositionibus principales diametri non tantum axes, sed et simpliciter diametri possunt intelligi: ita ut non solum ex axibus ipsis, sed etiam ex simplicibus diametris, ad quas ordinate ductae non sunt ad rectos, possint praedicto modo fieri ex generatione diametri: item ex ipsis⁸²⁸ factis ex generatione diametris eodem modo⁸²⁹ aliae ex generatione diametri fieri: quandoquidem hactenus demonstrata communia sunt axibus et simplicibus diametris.

Ex quibus quidem rursus patet, quod linea tangens sectionem, sive parabolen, sive hyperbolen, sive ellipsim, circulumve apud extremum diametri ordinate ducta est, quandoquidem aequidistat bifariam sectis a diametro, et perinde ordinate ductis.