[A:25r] 43^a Si hyperbolen, vel ellipsim vel circuli periferiam linea tangens coincidat diametro: et a tactu applicetur linea ordinate ad diametrum: et huic per summitatem aequedistans ducatur coincidens lineae per tactum et centrum ductae: a relicto autem puncto in sectione agantur duae lineae ad diametrum, quarum haec quidem penes⁶⁰⁰ tangentem, illa vero penes⁶⁰¹ ductam a tactu; factum sub ipsis triangulum minus erit quam triangulum, quod abscindit acta penes⁶⁰² ducta a tactu, in triangulo, quod adiacet ei, quae ex centro, similiter abscisum⁶⁰³ ab ea, quae per summitatem. In hyperbole: at in ellipsi et circulo, factum sub ipsis actis triangulum, cum ipso, quod acta⁶⁰⁴ penes ductam⁶⁰⁵ a tactu abscindit, triangulo, aequale erit ei, quod ad eam⁶⁰⁶, quae ex centro, ab ea, quae per summitatem similiter abscisum⁶⁰⁷ adiacet, triangulo.

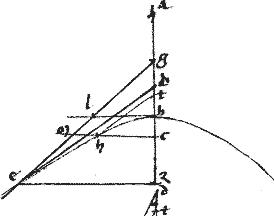
Sit hyperbole, ellipsis, circulusve cuius diameter ab. // Centrum g. // Tangens de.

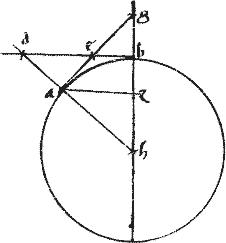
// Eique parallelus th⁶⁰⁸ // Per relictum contingenter punctum h. // Ordinate ductae ez hcm bl.

// Dico iam quod in hyperbola gcm aequale est gbl tch simul609.

In ellipsi vero et circulo gcm tch simul aequalia sunt gbl .

// Nam per 39am huius ratio ez zd componitur ex rationibus gz ze rectae transversam .

// Sed propter linearum aequidistantiam et ^lorum similitudinem ez zd sicut⁶¹⁰ hc ct. Itemque gz ze sicut⁶¹¹ gb bl.

// Igitur ratio hc ct componetur612 ex rationibus gb bl rectae transversam .

// Quare, quoniam, quod 41^a613 huius [A:25v] de parallelogrammis aequiangulis ostendit, idem de triangulis talium parallelogrammorum dimidiis dici potest.

Ideo // in hyperbola species, quae sit ex cg hoc est gcm similis speciei, quae sit ab ipsa bg hoc est ^lo gbl aequalis est aequiangulis invicem speciebus, quae ab ipsis bg ch fiunt, hoc est ^lis gbl tch. Quod est propositum.

// In ellipsi autem

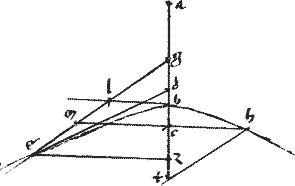
et circulo

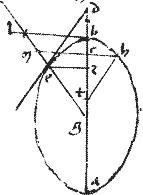
per eamdem 41^am quod sit ex gc hoc est gcm simile ei, quod ex bg hoc est gbl cum aequiangulo, quod ex ch hoc est tch aequum est ei, quod sit ex bg ipsi scilicet gbl. // Quod erat demonstrandum.

Scolium

Notandum quod tch dicitur esse aequiangulum ^lis gcm gbl [S:36] ob id solum, quod parallelogramma eorum dupla sunt aequiangula: quemadmodum 41^a huius ratiocinatur. Item propter varium situm⁶¹⁴ puncti h contingenter relicti, tam in hyperbola, quam in ellipsi, circuloque descriptio tripliciter variatur.

[A:26r] Si in contrapositis linea per centrum ducta utrique sectioni coincidat: lineae, quae apud coincidentias tangunt sectiones, sunt invicem aequidistantes.

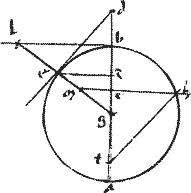
Sint contrapositae ad be. // Quarum diameter ab. // Centrum g. // Linea dge sectionibus incidens apud puncta d e. // Tangentes dz eh.

// Dico iam quod ipsae dz eh sunt invicem aequidistantes.

// Ordinate enim ducantur dt ec ad diametrum. // Et quoniam per 30^am huius, ipsae dg ge aequales: et ipsae dt ec aequidistantes. // Ideo iam aequilatera ad invicem erunt ipsa dtg etg. // Itaque latera [[qt]] [[qc]]⁶¹⁵

aequalia.

// Aequales autem ag gb. // Supersunt ergo⁶¹⁶ at bc aequales.

// Itaque ut bt ta sic ac cb.

Verum per 36^am huius sicut bt ta sic bz za et sicut ac cb sic ah hb. // Ergo sicut bz za sic ah hb. Et coniunctim sicut ba az sic ab bh.

Igitur per 9^am 5ⁱ Euclidis az bh sunt aequales. // Quare tota iam zt toti hc aequalis.

// Fuerunt autem et ec dt aequales et anguli ztd hce aequales propter aequidistantiam ipsarum td ce.

// Ergo, per 4^am primi Euclidis bases dz eh aequales: et caeteri anguli caeteris angulis aequales.

// Itaque anguli dzt ehc aequales.

// Quare per 28^am primi Euclidis bases⁶¹⁷ dz eh sunt aequidistantes. // Quod fuit demostrandum.

Et manifestum praeterea, quod ipsae dz eh⁶¹⁸ a diametris videlicet⁶¹⁹ ad tactuum⁶²⁰ puncta sunt invicem aequales⁶²¹

Scholium

Nota quod presens addita potuisset demonstrari per additam post 32^am huius. Nam cum dz eh tangant sectiones apud extrema diametri egd sunt iam ordinate ductae et perinde aequidistantes. Hoc tamen supposito quod dge sit diameter. Sed hic ab tantum supponitur diameter.

Item quod ipsae gz gh [A:26v] distantiae scilicet tangentium a centro sunt ad invicem aequales. Et ideo ipsa triangula (dgz egh invicem aequalia)⁶²² Quod si ponatur zd contingens: et ipsi gz aequalis gh et connectatur he stantibus caeteris⁶²³ // Aio quod et he tanget sectionem apud e.

Nam cum dz sit tangens, erit per 36^am huius bt ta sicut bz za. // Quare, propter aequalitatem linearum ex hypothesi erit et⁶²⁴ ac cb sicut ah hb⁶²⁵ et ideo per 34^am huius he tanget sectionem. Quod est propositum.

Rursus ponatur zd contingens: et ipsi gz aequalis gh et ducatur ipsi zd aequidistans hl stantibus caeteris.

// Aio quod hl producta tanget sectionem apud e.

Secus enim, sit me quae sectionem tangit apud e: cum autem et tangens sit dz. // Iam, sicut dudum ostensum est, tangentes aequaliter distabunt a centro: hoc est gm ipsi gz aequalis erit: sed gz ipsi gh aequalis per hypothesim. Igitur gh gm aequales: quod est absurdum.

// Non igitur alia quam hl sectionem apud e tanget, quod est propositum.

Item ponatur zd tangens: et ipsi gz aequalis gh. Et a puncto h ducatur linea quaedam sectioni coincidens ipsique zd aequalis [[stantibus caeteris]]. // Aio quod talis linea sectioni coincidet, ipsamque tanget apud e punctum hoc est, erit ipsa eadem he linea.

Nam, cum ipsa he sicut ostensum est, sectionem contingat apud e omnis alia linea a puncto h incidens sectioni brevior erit, quam ipsa he et perinde brevior, quam ipsa zd quod est contra hypotesim. Igitur talis linea non alia erit quam ipsa he et ideo, sicut ostensum est, tanget in puncto e sectionem. Quod est propositum.

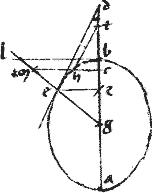
Adhuc ponatur zd tangens: et hl ei aequidistans⁶²⁶ producta tangat sectionem. // Aio quod tunc ipsi gz aequalis erit gh et ipsae tangentes aequales.

Unde tunc de conectens tactus ibit per g centrum.

Secus enim sit ipsi gz aequalis gm. // Et per m ducatur ipsi hl et perinde ipsi zd aequidistans linea, quae per antepraemissam⁶²⁷ continget sectionem, [S:37] incidens extra vel intra⁶²⁸ tangentem: quod est absurdum. // [[Omnino]] ergo gh ipsi gz aequalis. Et ideo per antepraemissam hl⁶²⁹ tanget sectionem apud e. // Quare, sicut prima demonstrat, tangentes aequales.