[S:34] 42a Si parabolen linea tangens coincidat diametro: et a tactu linea applicetur579 ad diametrum ordinate: et a relicto quodam puncto in sectione ducantur ad diametrum duae lineae, una quidem penes tangentem, altera penes applicatam580 a contactu; factum sub ipsis diametroque triangulum aequale est contento parallelogrammo sub applicata a tactu et recepta inter applicatae parallelum summitatemque sectionis.
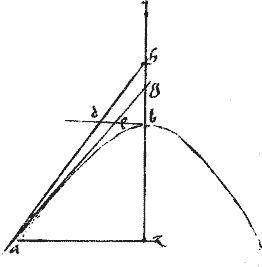
Sit parabole, cuius diameter ab. //
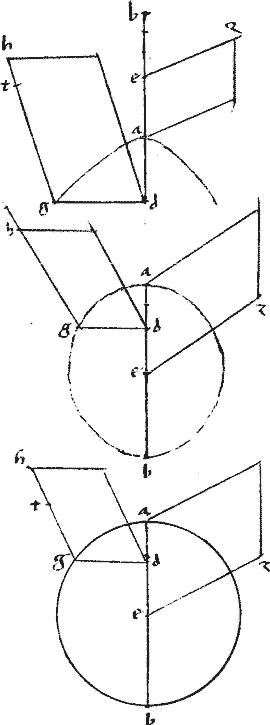
Tangens ag. // Ordinate ducta gt. // Relictum contingenter punctum d. //
// de581 penes ipsam ag. // dz penes ipsam gt. //582 //
// Dico iam quod583 ![]() dez
dez ![]() aequale est
aequale est ![]()
![]() gt bz.
6
// Ducatur enim penes ipsam gt, ipsa hb compleanturque parallelogramma hz zg. // Iam584 ostendendum est quod
gt bz.
6
// Ducatur enim penes ipsam gt, ipsa hb compleanturque parallelogramma hz zg. // Iam584 ostendendum est quod ![]() dez aequale est
dez aequale est ![]() zh585.
zh585.
// Cum enim per 35 am huius ab aequalis sit bt erit per 41am primi Euclidis ![]() atg aequum
atg aequum ![]() bg586.
bg586.
// Et quoniam, per 20am huius, ![]() gt
gt ![]()
![]() dz sicut tb
dz sicut tb ![]() bz.
bz.
// Et per 17am 6i Euclidis sic ![]() atg
atg ![]()
![]() ezd.
ezd.
// Et per primam sexti Euclidis
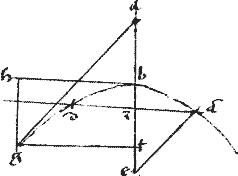
sic ![]() bg
bg ![]()
![]() zh587 estque
zh587 estque ![]() atg aequum
atg aequum ![]() bg588.
bg588.
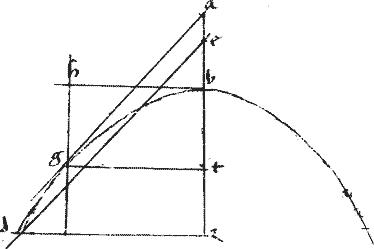
// Ideo per 14am quinti Euclidis et ![]() dez aequale erit
dez aequale erit ![]() zh589. // Quod fuit demonstrandum.
zh589. // Quod fuit demonstrandum.
COROLLARIUM
Et manifestum fuit quod in parabola trigonum, quod facit una tangentium [[cum]] diametro per reliquum tactum eiusque ordinata, aequale est parallelogrammo, quod sub dicta ordinata ac segmento dictae diametri ab ordinata ad tactum usque recepto continetur.
Si hyperbolen, ellipsim, circulumve lineae tangant se vicissim590 secantes, et utraque diametro per alterius contactum ductae coincidentes;591 facta triangula communem angulum in centro habentia sunt ad invicem aequalia.
Sit hyperbole, ellipsis, vel circulus ab cuius diameter bh. // Centrum h. // Tangentes ga db
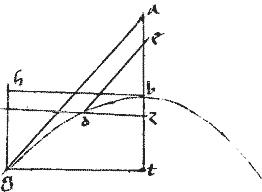
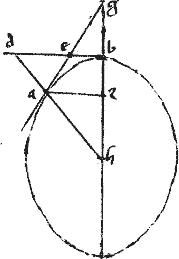
se invicem apud e secantes. // Tactuum puncta a b. // Diametri hbg had592.
// Dico iam quod ![]()
![]() agh bdh sunt invicem aequalia.
agh bdh sunt invicem aequalia.
// Ducatur enim penes bd recta az eritque per additam 32ae ipsa db et perinde az ordinate ducta.
// Quare per 37am huius ![]() ghz aequale est
ghz aequale est ![]() bh et ideo per 16am sexti Euclidis zh
bh et ideo per 16am sexti Euclidis zh ![]() hb
hb ![]() gh sunt in proportione continua.
gh sunt in proportione continua.
Et per 17am eiusdem sicut zh ![]() hg sic
hg sic ![]() zh
zh ![]()
![]() hb.
hb.
Verum sicut ![]() zh
zh ![]()
![]() hb sic
hb sic ![]() 593 ahz
593 ahz ![]()
![]() dh[[b]]594 quandoquidem similes, similiterque creatae figurae sunt proportionales per 18am 6i Euclidis.
dh[[b]]594 quandoquidem similes, similiterque creatae figurae sunt proportionales per 18am 6i Euclidis.
Atque per primam eiusdem sicut zh ![]() hg sic
hg sic ![]() ahz
ahz ![]()
![]() ahg595.
ahg595.
|
// Quare per 9am 5i Euclidis ![]()
![]() ahg dhb597 sunt invicem aequalia quandoquidem aequiangula. // Et ideo598
ahg dhb597 sunt invicem aequalia quandoquidem aequiangula. // Et ideo598 ![]()
![]() agh bdh parallelogrammorum dimidia, sunt invicem aequalia599.
agh bdh parallelogrammorum dimidia, sunt invicem aequalia599.
// Quod erat demonstrandum.