40a Si hyperbolen, vel ellipsim, vel circuli periferiam linea tangens coincidat secundae diametro: et a tactu applicetur linea ad eandem512 diametrum aequidistans alteri diametro: sumaturque utravis duarum linearum, quarum haec quidem inter applicatam et centrum sectionis, illa vero inter applicatam et tangentem; habebit ad sumptam513 applicata compositam rationem ex ea, quam habet reliqua duarum linearum ad applicatam, et ex ea, quam habet transversa ad rectam514.
Sit hyperbole, ellipsis, vel circulus, cuius diameter sit bzg. // Centrum z.
// Secunda diameter dze. // Tangens tla.
// Et ah parallelus ipsi bg.
|
|
//
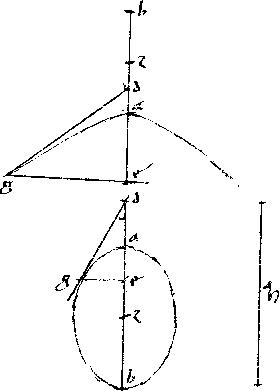
Sit enim ipso515 ![]() lo thz aequale
lo thz aequale ![]() hac. // Et quoniam per 38am praemissam,
hac. // Et quoniam per 38am praemissam, ![]() thz
thz ![]()
![]() ha sicut516 recta ad transversam. // Ideo et ipsum
ha sicut516 recta ad transversam. // Ideo et ipsum ![]() hac
hac ![]()
![]() ha sicut517 recta
ha sicut517 recta ![]() transversam et sic c
transversam et sic c ![]() ha per primam 6i Euclidis.
ha per primam 6i Euclidis.
//
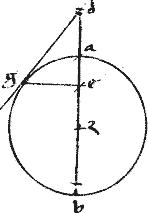
Et quoniam ![]()
![]() thz hac aequalia518 ideo per 15am 6i c
thz hac aequalia518 ideo per 15am 6i c ![]() hzsicut519 th
hzsicut519 th ![]() ha.
ha.
|
|
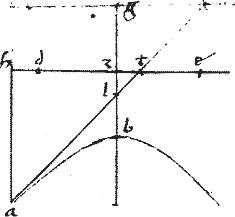
// Similiter per520 rationem ah ![]() hz sumentes rationem ah521
hz sumentes rationem ah521 ![]() ht ostendemus /
ht ostendemus /
|
// Sicut proponitur demonstrandum.