39a Si hyperbolen, vel ellipsim, vel circuli periferiam linea tangens coincidat diametro: et a tactu applicetur linea ad diametrum ordinate: sumaturque utravis duarum linearum, quarum haec quidem est inter applicatam et centrum sectionis: illa vero inter applicatam et tangentem: habebit ad sumptam504 applicata compositam rationem ex ea, quam505 reliqua duarum linearum506 ad applicatam, et ex ea, quam rectum507 speciei latus ad508 transversum.
Sit hyperbole, ellipsis,
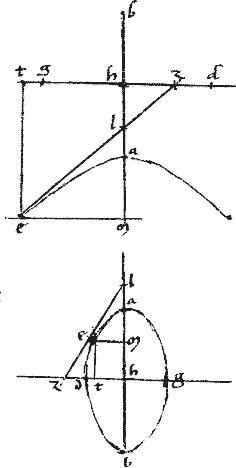
vel circulus, cuius diameter ab. // Centrum z. //
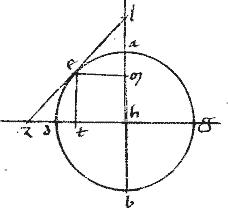
Tangens gd. // Or[S:32]dinate ducta ge.
|
|
// Sit enim ipsi
![]() zed aequale
zed aequale ![]() egh. // Et quoniam per antepremissam
egh. // Et quoniam per antepremissam ![]() zed
zed ![]()
![]() ge sicut transversa ad rectam. // Ideo erit et
ge sicut transversa ad rectam. // Ideo erit et ![]() egh
egh ![]()
![]() ge hoc est h
ge hoc est h ![]() ge sicut transversa ad rectam, et conversim.
ge sicut transversa ad rectam, et conversim.
// Et quoniam ![]()
![]() zed egh aequalia510 ideo per 15am 6i Euclidis ez
zed egh aequalia510 ideo per 15am 6i Euclidis ez ![]() eg sicut511 h
eg sicut511 h ![]() ed.
ed.
|
|
[A:22v] // Similiter pro ratione ge ![]() ed [[sumentes]] rationem ge
ed [[sumentes]] rationem ge ![]() ez demonstrabimus,
ez demonstrabimus,
|
// Quemadmodum proponitur demonstrandum.