[A:21v]

38^a. Si hyperbolen, vel ellipsim, vel circuli periferia linea tangens coincidat secundae diametro: et a contactu linea applicetur ad eandem⁴⁹¹ diametrum aequidistans alteri diametro; recepta linea sub applicata ad centrum sectionis, cum recepta sub tangente ad idem centrum aequale continebit rectangulum quadrato, quod sit ex dimidio secundae diametri: cum ea autem, quae est inter applicatam et tangentem continebit superficiem⁴⁹² rationem habentem ad id⁴⁹³, quod sit ex applicata, quam habet⁴⁹⁴, rectum speciei latus ad transversum.

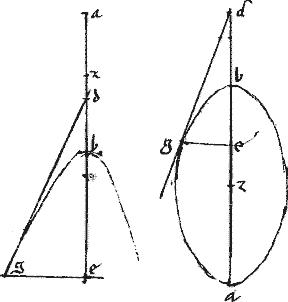
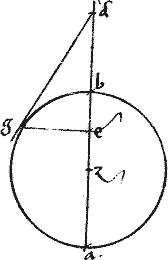
Sit hyperbole, ellipsis, vel circulus cuius diameter prima ab. // Secunda gd. // Centrum⁴⁹⁵ h.

// Tangens lez. // Et⁴⁹⁶ parallelus ipsi ab. // Ordinate ducta em.

// Dico iam quod zht aequum est ^to hd. // Item quod htz te est sicut recta trasversam.

// Nam per praecedentem; sicut hml⁴⁹⁷ me sic trasversa ad rectam.

//

Sed ex 13^ae corollario, transversa⁴⁹⁸ ba gd sicut⁴⁹⁹ gd rectam. Et ideo transversa rectam sicut ab gd vel ha hg.

// Igitur sicut ha hg sic hml me.

// Sed ratio hml me componitur ex rationibus hm me vel ht lm me .

// Ergo ratio ha hg componitur ex iisdem. //

Et conversim ratio gh ha500 componetur ex rationibus th em mh em ml vel zh hl 501 .

// Sed ea est ratio zht mhl.

// Igitur zht mhl sicut gh ha⁵⁰². // Et permutatim zht gh sicut mhl ha.

// Verum per praemissam mhl aequum ha. // Ergo et zht aequum erit gh

vel hd. // Quod fuit primum ex demonstrandis. [A:22r] Rursus, quoniam ex praecedenti, recta ad transversam sicut⁵⁰³ em hml.

// Et ratio em hml componitur ex rationibus em hm et ideo ex rationibus ht te em ml zt te

ex quibus quidem rationibus iam pridem componitur ratio zth te.

// Ideo zth te sicut recta transversam. Quod iam supererat demonstrandum.