37^a Si hyperbolen, vel ellipsim, vel circuli periferiam linea attingens coincidat diametro: et a tactu ad diametrum ducatur linea ordinate; recepta linea sub applicata ultra⁴⁷⁴ ad centrum sectionis cum recepta sub tangente ad centrum usque sectionis aequale continebit⁴⁷⁵ ei,⁴⁷⁶ quod sit ab ea, quae ex centro sectionis: cum ea autem, quae est inter applicatam et tangentem, continebit superficem⁴⁷⁷ habentem rationem ad id⁴⁷⁸, quod sit ex [S:31] applicata, quadratum⁴⁷⁹, quam transversum latus ad rectum.

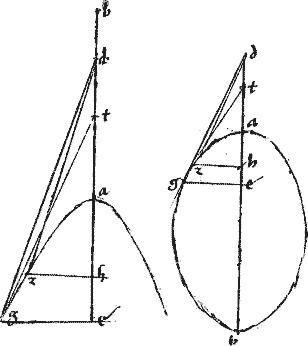
Sit hyperbole, vel ellipsis, vel circulus, cuius diameter ab. // Tangens gd. // Ordinate applicata ge. // Centrum z.

// Dico iam quod dze aequale est ^to zb. // Itemque quod dez eg sicut⁴⁸⁰ transversum ad rectum speciei latus.

// Nam, per precedentem, erit [A:21r] sicut ad db sic ae eb.

// Et coniunctim sicut adb bd sic aeb eb.

// Sed in hyperbola zb 1/2 ipsius adb. Itemque ze 1/2 utriusque ae eb.

// Igitur ze eb sicut zb bd. // 1 Et permutatim⁴⁸¹

ze zb sicut eb bd. // Et disiunctim zb be sicut zd db. // Et permutatim zb zd sicut eb bd. 2 // Quare ze zb sicut zb zd. Et iam per 16^am 6ⁱ Euclidis ezd aequale zb in hyperbola. // Et quoniam sicut ze eb sicut⁴⁸² zb sive az bd erit permutatim az ze sicut bd eb. Et coniunctim ae ez sicut de eb.

// Et ideo per 15^am 6ⁱ Euclidis aeb aequale zed.

// Sed per 21^am huius aeb eg sicut⁴⁸³ transversum ad rectum speciei latus.

// Igitur et zed eg erit itidem, sicut transversum ad rectum speciei latus in hyperbola. In ellipsi autem

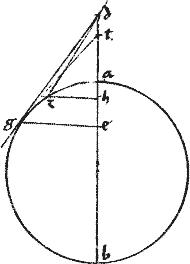
et circulo ipsius adb 1/2 est ipsa zd. // Et ipsius ab 1/2 est zb.

// Quare zd db sicut⁴⁸⁴ zb eb.

3 // 4 Et permutatim⁴⁸⁵ zd zb sicut db be. // Et conversim zb zd sicut eb bd. Et disiunctim zb bd sicut ze eb. // Et permutatim ze zb sicut eb bd. 5 // Igitur ze zb sicut zb zd. // Rursum ergo per 16^am 6ⁱ ezd aequale est zb in ellipsi et circulo.

// Sed per primam 2i486 Euclidis ezd dez ze

et per 5am eiusdem bz aeb ze aequale est.

// Ergo dez et ze ze simul aequalia sunt ^lo aeb et ze simul sumptis.

// Commune auferatur ze et supererunt dez aeb invicem aequalia. // Sed per 21^am huius aeb eg sicut transversa⁴⁸⁷ ad rectam⁴⁸⁸. // Igitur et dez ge sicut transversa⁴⁸⁹ ad rectam⁴⁹⁰ in ellipsi et circulo: sicut proponitur demonstrandum.