36a Si hyperbolen vel ellipsim vel circuli periferiam tangat quaedam linea coincidens transverso speciei lateri: et a tactu ducatur linea ordinate ad diametrum; erit, ut467 recepta sub tangente ad extremum transversi lateris, ad receptam sub tangente ad alterum extremum lateris, sic468 recepta sub applicata ad extremum ad receptam sub applicata ad alterum extremum lateris: quare eiusdem rationis continuas esse.469 Et inter tangentem et sectionem alia linea non intercidet.
Sit hyperbole, ellipsis vel circulus, cuius diameter ab. // Tangens autem gd. // Ordinate ducta ge.
// Dico iam quod est sicut be ![]() ea sic bd
ea sic bd ![]() da.
da.
// Si enim non sit.
// Ponatur iam ut470 bd ![]() da [A:20v] sicut bh
da [A:20v] sicut bh ![]() ha. // Et ordinate ducatur hz.
ha. // Et ordinate ducatur hz.
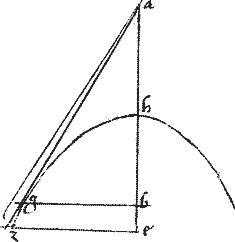
dz coniuncta tanget471 sectionem in ipso z puncto, cadensque extra sectionem occurret producta ipsi dg. // Eruntque duarum rectarum iidem termini. // Quod est absurdum.
// Omnino ergo erit, sicut be ![]() ea sic bd
ea sic bd ![]() da.
da.
// Quod est primum ex demonstrandis.
// Dico item quod inter sectionem ag et tangentem gd alia linea non intercidet. // Si enim possibile est, intercidat gt.
// Itaque tangens erit gt. // Et ordinate ducta ge.
// Quare per praesentem propositionem, erit sicut be ![]() ea sic bt
ea sic bt ![]() ta
ta
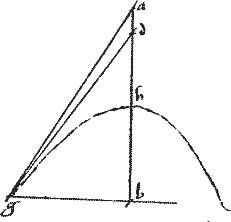
.
// Fuit autem sicut be ![]() ea sic bd
ea sic bd ![]() da. // Igitur sicut bd
da. // Igitur sicut bd ![]() da sic bt
da sic bt ![]() ta.
ta.
Et coniunctim sicut472 ab ![]() da sic ab
da sic ab ![]() ta.
ta.
// Quare per 9am 5i [S:30] Euclidis da at ad invicem equales473: quod est impossibile. // Inter sectionem igitur et tangentem linea non intercidit. // Quod demonstrandum supererat.