35a Si parabolen linea tangat coincidens diametro extra sectionem; ducta a tactu linea ordinate ad diametrum aequalem recipiet ex diametro ad summitatem sectionis, ei quae a summitate ad tangentem. [S:29] Et inter locum tangentis et sectionem nulla linea intercidet.
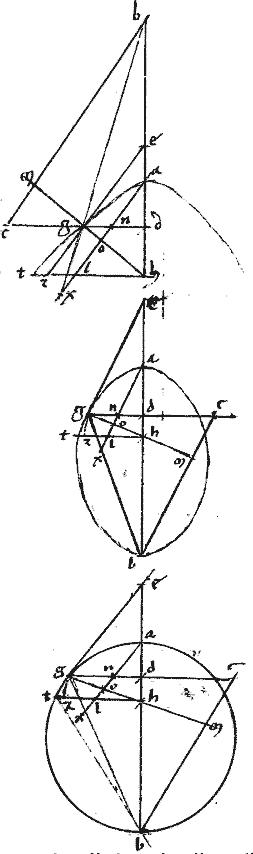
Sit parabole, cuius diameter ab ordinate ducta gb. // Et ipsa ga tangat sectionem in puncto g.
// Dico iam quod ipsa ah461 aequalis est ipsi hb. // Sit enim, si possibile est, hb maior minorve quam ah462. // Ponaturque ipsi ah aequalis he. // Et ordinate ducatur ez.
Itaque per 33am praecedentem az in ipso z puncto tanget sectionem, et producta cadet extra sectionem. // Quare
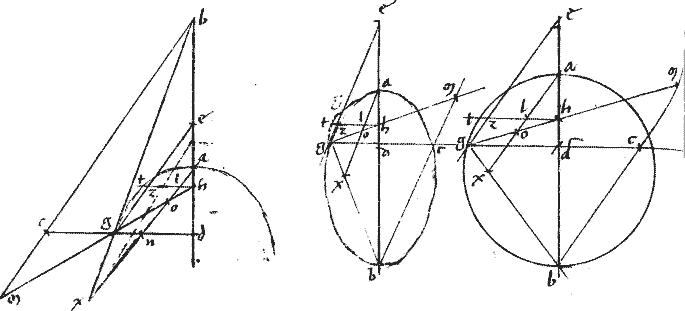
[[si]]463 z contactus [A:20r] superior sit ipso g contactu: iam ipsa az post conctatum sectionis, occurret ipsi ag lineae cadens videlicet extra sectionem.
// Si vero z tactus sit infra ipsum g tactum: tunc ipsa az cadens extra sectionem cadet, omnino extra ipsam ag properansque ad tactum z occurret ante tactum ipsi ag tangenti et extra sectionem cadenti. // Quo fiet, ut duarum rectarum iidem sint termini: quod est absurdum. // Non est ergo hb maior nec464 minor quam ah465. Aequalis igitur, quod erat demonstrandum.
// Dico etiam quod
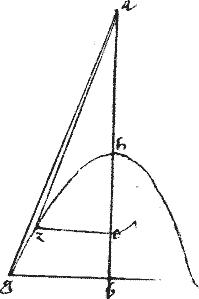
inter ag tangentem, atque ipsam periferiam gh nulla linea intercidet.
// Cadat enim, si possibile est gd itaque gd extra periferiam cadens, continget sectionem in puncto g in quo quidem secans ipsam ag producta deinde, tam extra ag productam quam extra sectionem incedet. // Itaque cum tangens sit dg et ordinate ducta gb iam per praesentem propositionem, aequalis erit dh ipsi hb. //
Fuit autem et ipsi hb aequalis ipsa ah. // Aequales ergo erunt ah hd. // Quod est impossibile. // Igitur inter sectionem et ipsam ag tangentem nulla linea intercidit466. // Quod supererat demonstrandum.