34a Si in hyperbole, vel ellipsi, vel circuli periferia relictum sit quoddam438 punctum: et ab ipso ducatur linea ad diametrum ordinate: et quam habent rationem ad invicem abscisae439 sub applicata ad terminos transversi speciei lateris, eadem habeant receptae sub puncto extrinseco ad praedictos terminos, ex eodem transverso latere; quae punctum extrin[S:28]secum cum puncto in periferia relicto coniungit, linea tanget in ipso puncto sectionem.
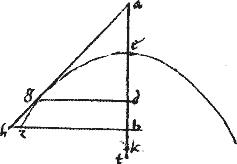
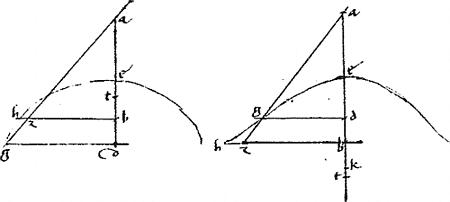
Sit hyperbole, ellipsis, circulusve, cuius diameter ab. // Et a contingenter relicto puncto g in periferia ordinate ducatur gd. // Sitque sicut bd ![]() da sic be
da sic be ![]() ea. // Et connectatur eg.
ea. // Et connectatur eg.
// Dico iam, quod eg tanget sectionem in ipso g puncto.
// Secet enim, si possibile est. Sitque egz et a quodam puncto z ordinate applicetur hzt. // Item agantur al bc penes ipsam ag440. // Et coniungantur bg gh incidentes ipsis al bc apud xom. // Ipsae autem al bc incidant ipsi gd apud nc. // Et al ipsi hzt apud l.
// Et, quoniam propter linearum aequidistantiam / et ![]()
![]() similitudinem bd
similitudinem bd ![]() da sicut441 bc
da sicut441 bc ![]() an.
an.
// Et ideo [A:19r] per hypothesim bc ![]() an sicut be
an sicut be ![]() ea et be
ea et be ![]() ea sicut442 bg
ea sicut442 bg ![]() gx.
gx.
// Et bg ![]() gx sicut bc
gx sicut bc ![]() xn.
xn.
|
// Quare per 9am 5i Euclidis an xn sunt aequales. // Et ideo ![]() anx maius444
anx maius444 ![]() lo aox.
lo aox.
// Et perinde maior445 nx ![]() xo quam oa
xo quam oa ![]() an sed nx446
an sed nx446 ![]() xo sicut447 cb
xo sicut447 cb ![]() bm.
bm.
// Igitur maior448 cb ![]() bm quam oa
bm quam oa ![]() an quare
an quare ![]() cb an maius449
cb an maius449 ![]() lo mb ao.
lo mb ao.
// Et ideo maius450 ![]() cb an
cb an ![]()
![]() ge quam
ge quam ![]() mb ao
mb ao ![]()
![]() ge.
ge.
// Verum propter similitudinem ![]()
![]() bcd egd
bcd egd ![]() cb an
cb an ![]()
![]() ge sicut451
ge sicut451 ![]() bda
bda ![]()
![]() de.
de.
// Itemque propter similitudinem ![]()
![]() bmh egh
bmh egh ![]() mb ao
mb ao ![]()
![]() ge sicut452
ge sicut452 ![]() bha
bha ![]()
![]() he.
he.
// Ergo maius453 ![]() bda
bda ![]()
![]() de quam
de quam ![]() bhe454
bhe454 ![]()
![]() he.
he.
// Et permutatim maius ![]() 455 bda
455 bda ![]()
![]() bha quam
bha quam ![]() de
de ![]()
![]() he.
he.
// Sed per 21am huius ![]() bda
bda ![]()
![]() bha sicut456
bha sicut456 ![]() gd
gd ![]()
![]() th.
th.
// Et propter ![]()
![]() edg ehz similitudinem sicut
edg ehz similitudinem sicut ![]() de
de ![]()
![]() eh sic
eh sic ![]() gd
gd ![]()
![]() zh.
zh.
// Quare et ![]() gd maius457 ad
gd maius457 ad ![]() th quam ad
th quam ad ![]() zh.
zh.
// Et ideo per 10am 5i Euclidis ![]() zh maius458
zh maius458 ![]() to th. // Et ipsa zh maior, quam ht.
to th. // Et ipsa zh maior, quam ht.
// Quod est impossibile.
// Igitur eg producta extra sectionem cadet. // Et similiter ostendemus, quod neque supra punctum g secabit periferiam: ducta videlicet ipsa tzh supra ipsam gd caeterisque, ut prius. // Quare eg in ipso solum [A:19v] g puncto tangit sectionem.
// Quod erat demonstrandum.
Scholium
// Quod si obiiceret adversarius, quod eg secat periferiam sectionis supra g punctum: tunc ducta459 tzlh linea supra ipsam gd caeterisque, ut prius, iisdem repetitis argumentis confutaretur. // Et [[ecce]] iam hic expositas ei casui accommodatas figurationes460.