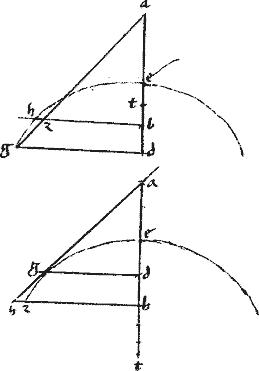
33^a Si in paraboles periferia relictum sit quoddam⁴¹⁰ punctum, et ab ipso ordinate ad diametrum linea applicetur: et receptae⁴¹¹ sub ipsa ex dia[S:27]metro ad summitatem ponatur aequalis linea in rectum a summitate; quae a termino huius lineae ad relictum punctum coniungitur, in ipso relicto puncto tanget sectionem

Sit parabole, cuius diameter ab. // Relictum in periferia g. // Ordinate ducta gd. // Ipsique de ponatur aequalis ea. // Et connectatur ag. //

// Dico iam quod ag producta extra sectionem cadet.

// Cadat enim, si possibile est intus, ut⁴¹² gz secetque primum sectionem supra g punctum. // Et agatur bzh penes dg. // Sintque da ba ta in proportione continua.

Eritque, per 17^am 6ⁱ Euclidis da ba et ideo, propter⁴¹³ similitudinem et aequidistantiam linearum, [A:18r] dg bz sicut da at.

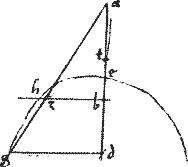
// Et quoniam da totum ba totum⁴¹⁴, sicut ba abscisum⁴¹⁵ ta abscisum⁴¹⁶.

// Ideo, per 19^am 5ⁱ Euclidis bd reliquum bt reliquum⁴¹⁷, sicut da totum ba totum.

// Maius⁴¹⁸ autem da quam ba ergo et bd maius, quam bt.

// Unde sit, ut, quoniam ad ipsius de dupla est, hoc est totum totius: ipsa vero dt ipsius db minor, quam dupla, abscisum⁴¹⁹ videlicet abscissi; erit per 33^am quinti additam a Campano, at ipsius be maior, quam dupla, residuum scilicet residui. Maior⁴²⁰ ergo at be quam ad de.

// Et permutatim maior at ad quam be de.

Verum fuit sicut ta ad sic bz dg. // Et per 20^am421 huius, sicut be ed sic bh dg.

// Igitur maius⁴²² bz dg quam bh dg.

// Quare per 10^am quinti Euclidis bz maius^{423 to} bh. // Et ideo bz maior, quam bh. // Quod est absurdum. Cadat deinde ag in ipso primum g puncto intra parabolam, si possibile est. Et ordinate agatur bzh infra ipsam dg. // Sintque da ba ta in proportione continua: quarum maxima ta.

// Eritque per 17^am 6ⁱ Euclidis da ba et ideo propter similitudinem dg bz sicut da at.

// Et, quoniam ta totum ab totum sicut ba abscisum⁴²⁴ ad abscisum⁴²⁵: ideo, per 19^am 5ⁱ tb reliquum bd reliquum sicut ta totum ab totum.

// Maius⁴²⁶ autem ta quam ab.

Ergo tb maius⁴²⁷, quam bd. // Unde⁴²⁸ quoniam ed ipsius da dimidium est⁴²⁹: ipsum vero bt ipsius td⁴³⁰ maius, quam dimidium: erit⁴³¹ per 13^am quinti eb ipsius at minus, quam dimidium.

// Nam si ponatur ipsi bd aequalis bk iam, cum ed sit 1/2 ipsius da itemque db 1/2⁴³² ipsius dk erit, per dictam 13^am totum eb iam 1/2 totius ak et ideo minus, quam 1/2⁴³³ ipsius at.

// Maior ergo erit⁴³⁴ de da quam eb at.

// Et permutatim maior⁴³⁵ de eb quam da at.

Est autem per 20^am huius sicut [A:18v] de eb sic dg bh⁴³⁶ fuitque sicut da at sic dg bz. //

Igitur

// maius erit⁴³⁷ dg bh quam dg bz.

// Quare, per 10^am quinti Euclidis bz maius est ^to bh. // Et ideo bz maior, quam bh. // Quod est absurdum.

// Itaque ag tam supra ipsum g punctum, quam infra tota extra periferiam sectionis cadet. Et perinde ipsam sectionem tanget. Apud ipsum g punctum. // Quod erat demonstrandum.