32a Si coni sectionis per summitatem linea ordinate applicata ducatur; tanget sectionem: et in eum locum, qui est inter coni sectionem et lineam, alia linea non intercidit395 .
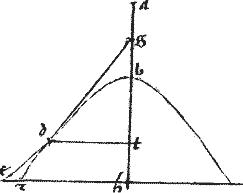
Sit coni sectio, cuius diameter ab. // Et ad diametrum ordinate ducta ag. // Quae per 17am huius tanget sectionem.
// Dico iam quod inter ag lineam et sectionem nulla linea intercidet396. //
// Cadat enim inter eas, si possibile est da. // Et a contingenti puncto d ordinate agatur ipsa dhe.
// Sitque az ad quam possunt ordinate ductae.
// Eritque primum in parabola [A:17r] ![]() 397 de
397 de ![]()
![]() ea398 maius399 quam
ea398 maius399 quam ![]() he sive
he sive ![]() eaz
eaz ![]()
![]() ea.
ea.
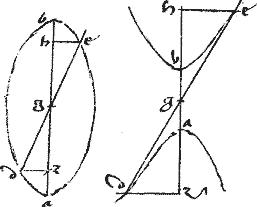
// Sed per primam 6i Euclidis ![]() eaz
eaz ![]()
![]() ea sicut400 za
ea sicut400 za ![]() ae.
ae.
// Igitur ![]() de
de ![]()
![]() ea maius401, quam za
ea maius401, quam za ![]() ae.
ae.
// Sit ergo sicut ![]() de
de ![]()
![]() ea sic za
ea sic za ![]() at.
at.
// Et ducatur tlc penes ipsam de.
// [S:26] Eritque propter similitudinem ![]()
![]() aed atc sicut
aed atc sicut ![]() de
de ![]()
![]() ea sic
ea sic ![]() ct
ct ![]()
![]() ta et per primam 6i Euclidis sicut za
ta et per primam 6i Euclidis sicut za ![]() at sic
at sic ![]() zat
zat ![]()
![]() at.
at.
// Quare sicut ![]() ct
ct ![]()
![]() ta sic
ta sic ![]() zat
zat ![]()
![]() at.
at.
// Sed per 11am huius, ![]() lt aequale402
lt aequale402 ![]() zat. // Igitur sicut
zat. // Igitur sicut ![]() ct
ct ![]()
![]() ta sic
ta sic ![]() lt
lt ![]()
![]() ta.
ta.
// Ergo per 9am 5i Euclidis, ![]()
![]() ct lt aequalia403. // Quod est absurdum.
ct lt aequalia403. // Quod est absurdum.
In hyperbola vero, ellipsi404, circulove agatur em penes ipsam az et occurrat ipsi bz apud m.
// Eritque per 12am vel 13am ![]() he aequale
he aequale ![]() aem.
aem.
// Sit ergo ![]() aen aequale
aen aequale ![]() to de. // Et coniungatur an secans ipsam bz apud x. // Et agatur xt penes az. // Et tlc penes de. // Eruntque, per 16am 6i ne
to de. // Et coniungatur an secans ipsam bz apud x. // Et agatur xt penes az. // Et tlc penes de. // Eruntque, per 16am 6i ne ![]() de
de ![]() ea in proportione continua.
ea in proportione continua.
// Quare, per 17am 6i sicut ne ![]() ea vel xt
ea vel xt ![]() ta sic
ta sic ![]() de
de ![]()
![]() ea et
ea et ![]() ct
ct ![]()
![]() ta. // Quare xt
ta. // Quare xt ![]() tc
tc ![]() ta sunt continue proportionales.
ta sunt continue proportionales.
// Et ideo, per 16am 6i ![]() xta quod est405 per 12am vel 13am
xta quod est405 per 12am vel 13am ![]() lt aequale est
lt aequale est ![]() tc. // Quod est absurdum.
tc. // Quod est absurdum.
// Igitur inter ag lineam et sectionem nulla linea intercidet406. // Quod est demonstrandum.
// Scholium
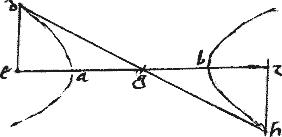
Sed quid, si ad non cadat inter ag et sectionem, scilicet secet, sicut re vera secat, ipsam ah sectionem? Sequeturne, veritate admissa, eadem absurditas [A:17v] ut scilicet tl tc sint aequales? Dicendum quod utrumque punctorum c l cadit in unum idemque punctum in quo videlicet ad linea secat sectionem. Atque ita tl tc sunc una et eadem linea. Quare nec absurditas locum habet. // Immo et hac via407 confutari potest adversarius408: sic enim ostenditur quod ipsa tl occurrit ipsi ad in illo eodem puncto in quo ad secat periferiam sectionis: sed cum ipsa ad et in alio puncto scilicet a incidat periferiae409; iam per 10am huius secabit sectionem: et perinde non cadet inter sectionem et lineam ag et similiter ostendetur, quod nulla linea inter tangentem lineam, et periferiam sectionis intercedet. Sicut proponitur demonstrandum.
Quae apud extremum diametri tangit sectionem, ordinate ducta est.
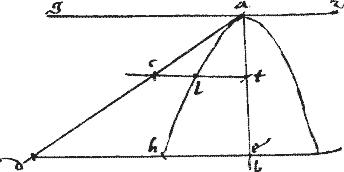
Haec est conversa praesentis propositionis. // Sit enim coni sectio ab cuius diameter bg. // Tangens db. //
// Dico iam quod db ordinate ducta est ad diametrum.
// Secus enim
sit ordinate ducta eb. // Igitur per 17am huius eb continget sectionem: cadet enim extra periferiam.
// Quare inter tangentem db et periferiam ab intercedet linea eb. // Quod per praesentem est impossibile.
// Itaque non alia, quam db erit ordinate ducta per b punctum. // Quod erat demonstrandum.