30a Si in ellipsi, vel in contrapositis, linea ducatur per centrum in utramque coincidens sectioni; bifariam secabitur ad centrum.
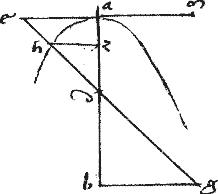
Ellipseos, vel contrapositarum diameter sit ab centrum vero g. // Per quod linea ducatur dge in utramque ad periferiam. // Dico quod gd aequalis est ipsi ge.
// Ducantur enim ordinate dz eh ad diametrum ab.
// Eritque per 21am huius ![]() bza
bza ![]()
![]() zd sicut382 transversa ad rectam. // Et similiter
zd sicut382 transversa ad rectam. // Et similiter ![]() ahb
ahb ![]()
![]() he; sicut transversa ad rectam. // Estque per 14am huius tam383 transversa, quam recta communis contrapositis384.
he; sicut transversa ad rectam. // Estque per 14am huius tam383 transversa, quam recta communis contrapositis384.
Igitur sicut ![]() bza
bza ![]()
![]() zd sic
zd sic ![]() ahb
ahb ![]()
![]() he. // Et permutatim
he. // Et permutatim ![]() bza
bza ![]()
![]() ahb sicut
ahb sicut ![]() zd
zd ![]()
![]() he. // Sed propter similitudinem
he. // Sed propter similitudinem ![]()
![]() sicut
sicut ![]() zd
zd ![]()
![]() he sic
he sic ![]() zg
zg ![]()
![]() gh.
gh.
// Ergo sicut [S:25] ![]() zg
zg ![]()
![]() gh sic
gh sic ![]() bza
bza ![]()
![]() ahb. // Et permutatim
ahb. // Et permutatim ![]() bza
bza ![]()
![]() zg sicut
zg sicut ![]() ahb
ahb ![]()
![]() gh.
gh.
|
|
// Propterea in ellipsi quidem coniunctim: in contrapositis vero vicissim et eversim et rursum vicissim argumentando, erit iam ![]() ag
ag ![]()
![]() zg sicut
zg sicut ![]() bg
bg ![]()
![]() gh // Sed
gh // Sed ![]() ag aequale385
ag aequale385 ![]() bg. // Igitur, per 14am 5i
bg. // Igitur, per 14am 5i ![]() zg aequale
zg aequale ![]() gh et perinde zg gh aequales. // Cumque dz h386 sint paralleli387: erunt
gh et perinde zg gh aequales. // Cumque dz h386 sint paralleli387: erunt ![]()
![]() dgz egh invicem aequilatera. // Quare gd aequalis ge quod erat demonstrandum.
dgz egh invicem aequilatera. // Quare gd aequalis ge quod erat demonstrandum.