29a Si365 hyperboles ad transversum latus speciei relictum sit quoddam366 punctum non minorem lineam recipiens ad summitatem sectionis dimidio transversi speciei lateris, et ab ipso coincidat linea ad [A:15v] sectionem; producta cadet intra sectionem ad id solum punctum incidens.
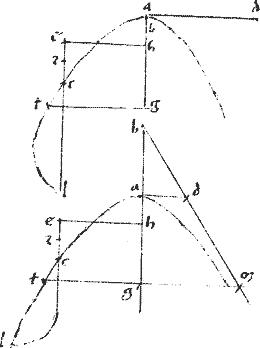
Sit hyperbole, cuius diameter ab in qua relictum g punctum recipiat bg non minorem dimidio ipsius ab.
// Et gd sectioni coincidat.
// Dico iam quod gd producta intra sectionem cadet ad ipsum ductaverat d punctum incidens.
// Cadat enim, si possibile est, extra sectionem, ut gde. // Et a relicto puncto e agatur ordinate ezh. // Sitque primum bg ipsius ab dimidium.
// Itaque quoniam ![]() eh
eh ![]()
![]() dt maiorem367 quam
dt maiorem367 quam ![]() zh
zh ![]()
![]() dt. // Atque propter similitudinem
dt. // Atque propter similitudinem ![]()
![]() ghe gtd
ghe gtd ![]() eh
eh ![]()
![]() dt sicut368
dt sicut368 ![]() hg
hg ![]()
![]() gt. // Et per 21am huius
gt. // Et per 21am huius ![]() zh
zh ![]()
![]() dt sicut
dt sicut ![]() ahb
ahb ![]()
![]() atb.
atb.
// Propterea ![]() hg
hg ![]()
![]() 369 gt maius370 quam
369 gt maius370 quam ![]() ahb
ahb ![]()
![]() atb. // Et permutatim
atb. // Et permutatim ![]() hg
hg ![]()
![]() ahb maius371 quam
ahb maius371 quam ![]() gt
gt ![]()
![]() atb.
atb.
// Et, quoniam per 6am 2i Euclidis cum sint ag gb aequales ![]() hg aequale372 est
hg aequale372 est ![]() ahb cum
ahb cum ![]() bg. // Itemque
bg. // Itemque ![]() gt aequale
gt aequale ![]() atb et
atb et ![]() bg.
bg.
// Propterea per 30am quinti Elementorum additam a Campano.
|
// Erit conversim minor ratio ![]() hg
hg ![]()
![]() bg quam ratio373
bg quam ratio373 ![]() gt
gt ![]()
![]() bg.
bg.
![]() gt maius erit quam374
gt maius erit quam374 ![]() hg375. // Et ideo gt maior quam gh pars videlicet toto: quod est impossibile.
hg375. // Et ideo gt maior quam gh pars videlicet toto: quod est impossibile.
// Igitur
gd non extra, sed intra sectionem cadet. // Et [[nihilo]]376 magis, quae a quovis puncto intra a g puncta posito, linea sectioni coincidet, intra sectionem cadet377. // Quod erat demonstrandum. // Sed neque [A:16r] gd ad plura quam unum, ipsum scilicet d punctum sectioni coincidet. // Nam si ad aliud punctum coincidet: iam producta, per 10am huius, rursus extra cadet; rursumque adversarius iisdem argumentis confutabitur. // Quare gd378 et omnis379 a puncto extra g punctum posito linea380 sectioni incidens sectionem secat ad unum solum punctum coincidens381. Sicut proponitur demonstrandum.