[A:14v] [S:23] 27a
Si paraboles diametrum linea secet intra sectionem; in utramque coincidet sectioni.
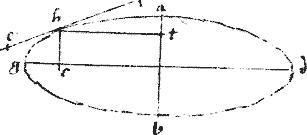
Paraboles diametrum ab secet intra sectionem linea dg.
// Dico iam quod dg utroversus338 producta coincidet sectioni.
// Ducatur enim a puncto a ordinate ae quae per 17am huius cadet extra sectionem.
// Itaque dg aut erit aequedistans ipsi339 ae vel non: si aequedistans: ergo ordinate applicatur. // Quare, per 19am340 huius, in utraque coincidet sectioni.
// Si autem dg aequedistans non sit ipsi ae coincidet341 ergo coincidat ad e. // Igitur coincidet prius periferiae sectionis, ut puta ad punctum h.
// Dico autem quod et in alias partes producta coincidet sectioni. // Sit enim, ad quam possunt ordinatae ductae, ipsa am.
// Sitque ![]() ad aequale
ad aequale ![]() zab.
zab.
// Eritque per 16am sexti Euclidis ba ![]() ad sicut ad
ad sicut ad ![]() az. Quare, per 19am 5i bd342
az. Quare, per 19am 5i bd342 ![]() dz reliqua scilicet ad reliquam sic ba
dz reliqua scilicet ad reliquam sic ba ![]() ad. // Et ideo
ad. // Et ideo ![]() bd
bd ![]()
![]() dz sicut
dz sicut ![]() ba
ba ![]()
![]() ad.
ad.
// Sed propter similitudinem ![]()
![]() et proportionem linearum, sicut
et proportionem linearum, sicut ![]() bd343
bd343 ![]()
![]() dz sic
dz sic ![]() bg
bg ![]()
![]() zh. // Et per 19am 6i344 Euclidis sicut ba
zh. // Et per 19am 6i344 Euclidis sicut ba ![]() az sic
az sic ![]() ba
ba ![]()
![]() ad et ideo sic
ad et ideo sic ![]() bd
bd ![]()
![]() dz. Quare sicut345
dz. Quare sicut345 ![]() bg
bg ![]()
![]() zh. //346 Et347 per primam 6i Euclidis sicut ba
zh. //346 Et347 per primam 6i Euclidis sicut ba ![]() az sic348
az sic348 ![]() bam
bam ![]()
![]() zam. Igitur sicut
zam. Igitur sicut ![]() bg
bg ![]()
![]() zh sic
zh sic ![]() bam
bam ![]()
![]() zam. // Et permutatim sicut
zam. // Et permutatim sicut ![]() bg
bg ![]()
![]() bam sic
bam sic ![]() zh
zh ![]()
![]() zam.
zam.
// Sed per 11am huius, ![]() zh aequale349
zh aequale349 ![]() zam. // Ergo
zam. // Ergo ![]() bg aequale350
bg aequale350 ![]() lo bam. // Cumque sit am recta ab vero transversa351 diameter. Veniet iam paraboles periferia per punctum g.
lo bam. // Cumque sit am recta ab vero transversa351 diameter. Veniet iam paraboles periferia per punctum g.
// Coincidet igitur dg sectioni apud g punctum. Quare dg in utramque352 producta coincidit sectioni: quod erat demonstrandum.
Scholium
Notandum quod haec coincidentia secantis353 diametrum propria est [A:15r] paraboles, non hyperboles: nam in hyperbola linea secans diametrum nonnunquam in unum ductaverat punctum coincidet periferiae.